初中数学相似多边形的性质填空题

在比例尺1∶10 000 000的地图上，量得甲、乙两个城市之间的距离是6 cm，那么甲、乙两个城市之间的实际距离应为        km.

若（x, y, z均不为0），则的值为           .

如图，点A₁，A₂，A₃，…，点B₁，B₂，B₃，…，分别在射线OM，ON上．OA₁=1，A₁B₁=2O A₁，A₁ A₂=2O A₁，A₂A₃=3OA₁，A₃ A ₄=4OA₁，…．A₁B₁∥A₂B₂∥A₃B₃∥A₄B₄∥…．则A₂B₂=          ，A_nB_n=               （n为正整数）．

在等腰梯形ABCD中，且AD=，∠B=45°.直角三角板含角的顶点E在边BC上移动，一直角边始终经过点A,斜边与CD交于点F．若是以AB为腰的等腰三角形，则CF的长等于              。

．如图，已知△中，=6，= 8，过直角顶点作⊥，垂足为，再过作⊥，垂足为，过作⊥，垂足为，再过作⊥，垂足为，…，这样一直做下去，得到了一组线段，，，…，则=         ，（其中n为正整数）=       ．  

如图:分别是的中点,,,分别是,,的中点这样延续下去.已知的周长是,的周长是,的周长是的周长是,则_____.
 

如图,已知两点A(2,0) , B(0,4) , 且∠1=∠2,则点C的坐标是__________?

如图，已知在△ABC中，AB=3，AC=2，D是边AB上的一 点，∠ACD=∠B，∠BAC的平分线AQ与CD、BC分别相交于点P和点Q，那么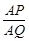的值等于  ▲  

已知在△ABC中，点D、E分别在边AB、AC上，DE//BC，，那么的值等于  ▲  ．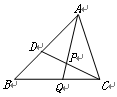

我们定义：“四个顶点都在三角形边上的正方形是三角形的内接正方形” ．
已知：在Rt△ABC中，∠C=90°，AC=6，BC=3．
（1）如图，四边形CDEF是△ABC的内接正方形，则正方形CDEF的边长a₁是            ；

（2）如图，四边形DGHI是（1）中△EDA的内接正方形，则第2个正方形DGHI的边长a₂=              ；继续在图2中的△HGA中按上述方法作第3个内接正方形；…以此类推，则第n个内接正方形的边长a_n=              ．（n为正整数）

一天，小青想利用影子测量校园内一根旗杆的高度，在同
一时刻内，小青的影长为2米，旗杆的影长为20米，若
小青的身高为1.60米,则旗杆的高度为           米．

数学兴趣小组想测量一棵树的高度，在阳光下，一名同学测得一根长为1米的竹竿的影长为0.8米，同时另一名同学测量一棵树的高度时，发现树的影子不全落在地面上，有一部分影子落在教学楼的墙壁上（如图），其影长为1.2米，落在地面上的影长为2.4米，则树高为        4.2米。

．如图，△ABC中，D，E分别为AC，BC边上的点，AB∥DE，CF为AB边上的中线，若AD=5，CD=3，DE=4，则BF的长为___________．

设抛物线与X轴交于两不同的点(点A在点B的左边)，与y轴的交点为点C(0,-2)，且∠ACB=90⁰．

（1）求m的值和该抛物线的解析式；
（2）若点D为该抛物线上的一点，且横坐标为1，点E为过A点的直线y=x+1与该抛物线的另一交点.在X轴上是否存在点P，使得以P、B、D为顶点的三角形与△AEB相似，若存在，求出点P的坐标，若不存在，请说明理由．
（3）连结AC、BC，矩形FGHQ的一边FG在线段AB上，顶点H、Q分别在线段AC、BC上，若设F点坐标为（t，0），矩形FGHQ的面积为S，当S取最大值时，连接FH并延长至点M，使HM=k·FH，若点M不在该抛物线上，求k的取值范围．

如图，△ABC中，D、E分别是BC、AC的中点，BF平分∠ABC，交DE于点F，若BC=6，则DF的长是   ▲  ，△EDC与△ABC的面积之比为  ▲