初中数学相似三角形的应用试题

如图，树 $\mathit{AB}$ 在路灯 $O$ 的照射下形成投影 $\mathit{AC}$ ，已知路灯高 $\mathit{PO}=5m$ ，树影 $\mathit{AC}=3m$ ，树 $\mathit{AB}$ 与路灯 $O$ 的水平距离 $\mathit{AP}=4.5m$ ，则树的高度 $\mathit{AB}$ 长是 $($ 　　 $)$

A．

$2m$

B．

$3m$

C．

$\frac{3}{2}m$

D．

$\frac{10}{3}m$

如图，在河对岸有一矩形场地 $\mathit{ABCD}$，为了估测场地大小，在笔直的河岸 $l$上依次取点 $E$， $F$， $N$，使 $\mathit{AE}\perp l$， $\mathit{BF}\perp l$，点 $N$， $A$， $B$在同一直线上．在 $F$点观测 $A$点后，沿 $\mathit{FN}$方向走到 $M$点，观测 $C$点发现 $\angle 1=\angle 2$．测得 $\mathit{EF}=15$米， $\mathit{FM}=2$米， $\mathit{MN}=8$米， $\angle \mathit{ANE}=45°$，则场地的边 $\mathit{AB}$为　　米， $\mathit{BC}$为　　米．

如图，三角板在灯光照射下形成投影，三角板与其投影的相似比为 $2:5$，且三角板的一边长为 $8\mathit{cm}$．则投影三角板的对应边长为 $($　　 $)$

A． $20\mathit{cm}$B． $10\mathit{cm}$C． $8\mathit{cm}$D． $3.2\mathit{cm}$

《九章算术》中记载了一种测量井深的方法．如图所示，在井口 $B$处立一根垂直于井口的木杆 $\mathit{BD}$，从木杆的顶端 $D$观察井水水岸 $C$，视线 $\mathit{DC}$与井口的直径 $\mathit{AB}$交于点 $E$，如果测得 $\mathit{AB}=1.6$米， $\mathit{BD}=1$米， $\mathit{BE}=0.2$米，那么井深 $\mathit{AC}$为　　米．

学校门口的栏杆如图所示，栏杆从水平位置 $\mathit{BD}$绕 $O$点旋转到 $\mathit{AC}$位置，已知 $\mathit{AB}\perp \mathit{BD}$， $\mathit{CD}\perp \mathit{BD}$，垂足分别为 $B$， $D$， $\mathit{AO}=4m$， $\mathit{AB}=1.6m$， $\mathit{CO}=1m$，则栏杆 $C$端应下降的垂直距离 $\mathit{CD}$为 $($　　 $)$

A． $0.2m$B． $0.3m$C． $0.4m$D． $0.5m$

如图1， $E$为矩形 $\mathit{ABCD}$的边 $\mathit{AD}$上一点，点 $P$从点 $B$出发沿折线 $\mathit{BE}-\mathit{ED}-\mathit{DC}$运动到点 $C$停止，点 $Q$从点 $B$出发沿 $\mathit{BC}$运动到点 $C$停止，它们运动的速度都是 $1\mathit{cm}/s$．若点 $P$、点 $Q$同时开始运动，设运动时间为 $t\left(s\right)$， $\mathit{\Delta BPQ}$的面积为 $y\left(c{m}^2\right)$，已知 $y$与 $t$之间的函数图象如图2所示．

给出下列结论：①当 $0<t⩽10$时， $\mathit{\Delta BPQ}$是等腰三角形；② $S_{\mathit{\Delta ABE}}=48c{m}^2$；③当 $14<t<22$时， $y=110-5t$；④在运动过程中，使得 $\mathit{\Delta ABP}$是等腰三角形的 $P$点一共有3个；⑤ $\mathit{\Delta BPQ}$与 $\mathit{\Delta ABE}$相似时， $t=14.5$．

其中正确结论的序号是　　．

为测量操场上旗杆的高度，小丽同学想到了物理学中平面镜成像的原理．她拿出随身携带的镜子和卷尺，先将镜子放在脚下的地面上，然后后退，直到她站直身子刚好能从镜子里看到旗杆的顶端 $E$，标记好脚掌中心位置为 $B$，测得脚掌中心位置 $B$到镜面中心 $C$的距离是 $50\mathit{cm}$，镜面中心 $C$距离旗杆底部 $D$的距离为 $4m$，如图所示．已知小丽同学的身高是 $1.54m$，眼睛位置 $A$距离小丽头顶的距离是 $4\mathit{cm}$，则旗杆 $\mathit{DE}$的高度等于 $($　　 $)$

A． $10m$B． $12m$C． $12.4m$D． $12.32m$

“今有井径五尺，不知其深，立五尺木于井上，从木末望水岸，入径四寸，问井深几何？”这是我国古代数学《九章算术》中的“井深几何”问题，它的题意可以由图获得，则井深为 $($　　 $)$

A．1.25尺B．57.5尺C．6.25尺D．56.5尺

如图，若要在宽 $\mathit{AD}$为20米的城南大道两边安装路灯，路灯的灯臂 $\mathit{BC}$长2米，且与灯柱 $\mathit{AB}$成 $120°$角，路灯采用圆锥形灯罩，灯罩的轴线 $\mathit{CO}$与灯臂 $\mathit{BC}$垂直，当灯罩的轴线 $\mathit{CO}$通过公路路面的中心线时照明效果最好，此时，路灯的灯柱 $\mathit{AB}$高应该设计为多少米（结果保留根号）？

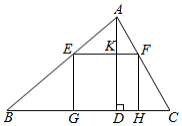
如图，一块材料的形状是锐角三角形 $\mathit{ABC}$，边 $\mathit{BC}=120\mathit{mm}$，高 $\mathit{AD}=80\mathit{mm}$，把它加工成正方形零件，使正方形的一边在 $\mathit{BC}$上，其余两个顶点分别在 $\mathit{AB}$、 $\mathit{AC}$上，这个正方形零件的边长是多少？

在如图所示的象棋盘（各个小正方形的边长均相等）中，根据“马走日”的规则，“马”应落在下列哪个位置处，能使“马”、“车”、“炮”所在位置的格点构成的三角形与“帅”、“相”、“兵”所在位置的格点构成的三角形相似 $($　　 $)$

A．①处B．②处C．③处D．④处

如图，在一斜边长 $30\mathit{cm}$的直角三角形木板（即 $\text{Rt}\Delta \text{ACB})$中截取一个正方形 $\mathit{CDEF}$，点 $D$在边 $\mathit{BC}$上，点 $E$在斜边 $\mathit{AB}$上，点 $F$在边 $\mathit{AC}$上，若 $\mathit{AF}:\mathit{AC}=1:3$，则这块木板截取正方形 $\mathit{CDEF}$后，剩余部分的面积为 $($　　 $)$

A． $200c{m}^2$B． $170c{m}^2$C． $150c{m}^2$D． $100c{m}^2$

《九章算术》是中国传统数学最重要的著作，在“勾股”章中有这样一个问题：“今有邑方二百步，各中开门，出东门十五步有木，问：出南门几步而见木？”

用今天的话说，大意是：如图， $\mathit{DEFG}$是一座边长为200步 $($ “步”是古代的长度单位）的正方形小城，东门 $H$位于 $\mathit{GD}$的中点，南门 $K$位于 $\mathit{ED}$的中点，出东门15步的 $A$处有一树木，求出南门多少步恰好看到位于 $A$处的树木（即点 $D$在直线 $\mathit{AC}$上）？请你计算 $\mathit{KC}$的长为　　步．

如图．利用标杆 $\mathit{BE}$测量建筑物的高度．已知标杆 $\mathit{BE}$高 $1.2m$，测得 $\mathit{AB}=1.6m$． $\mathit{BC}=12.4m$．则建筑物 $\mathit{CD}$的高是 $($　　 $)$

A． $9.3m$B． $10.5m$C． $12.4m$D． $14m$

如图，身高为1.8米的某学生想测量学校旗杆的高度，当他站在 $B$处时，他头顶端的影子正好与旗杆顶端的影子重合，并测得 $\mathit{AB}=2$米， $\mathit{BC}=18$米，则旗杆 $\mathit{CD}$的高度是　　米．