如图,线段 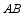 是
是 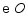 的直径,弦
的直径,弦 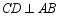 于点
于点 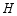 ,点
,点 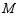 是
是 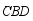 上任意一点,
上任意一点, 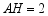 ,
, 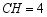 .
.
(1)求 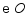 的半径
的半径 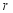 的长度;
的长度;
(2)求 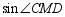 ;
;
(3)直线 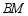 交直线
交直线 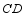 于点
于点 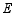 ,直线
,直线 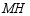 交
交  于点
于点 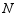 ,连接
,连接 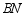 交
交 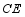 于点
于点 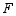 ,求
,求 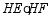 的值.
的值.
如图,在△ ABC中,∠ CAB=55°,∠ ABC=25°,在同一平面内,将△ ABC绕 A点逆时针旋转70°得到△ ADE,连接 EC,则tan∠ DEC的值是 .

如图,在矩形 ABCD中,点 E是 CD的中点,点 F是 BC上一点,且 FC=2 BF,连接 AE, EF.若 AB=2, AD=3,则cos∠ AEF的值是 .

如图,矩形 的四个顶点分别在直线 , , , 上.若直线 且间距相等, , ,则 的值为

A. B. C. D.
小明在某次作业中得到如下结果:
sin27°+sin283°≈0.122+0.992=0.9945,
sin222°+sin268°≈0.372+0.932=1.0018,
sin229°+sin261°≈0.482+0.872=0.9873,
sin237°+sin253°≈0.602+0.802=1.0000,
据此,小明猜想:对于任意锐角α,均有sin2α+sin2(90°-α)=1.
(Ⅰ)当α=30°时,验证sin2α+sin2(90°-α)=1是否成立;
(Ⅱ)小明的猜想是否成立?若成立,请给予证明;若不成立,请举出一个反例.
如图,在 中, , 和 关于直线 对称,连接 ,与 相交于点 ,过点 作 ,垂足为 , 相交于点 ,若 , ,则 的值为

A. B. C. D.
问题探究:
小红遇到这样一个问题:如图1, 中, , , 是中线,求 的取值范围.她的做法是:延长 到 ,使 ,连接 ,证明 ,经过推理和计算使问题得到解决.
请回答:(1)小红证明 的判定定理是: ;
(2) 的取值范围是 ;
方法运用:
(3)如图2, 是 的中线,在 上取一点 ,连结 并延长交 于点 ,使 ,求证: .
(4)如图3,在矩形 中, ,在 上取一点 ,以 为斜边作 ,且 ,点 是 的中点,连接 , ,求证: .

比萨斜塔是意大利的著名建筑,其示意图如图所示,设塔顶中心点为点 ,塔身中心线 与垂直中心线 的夹角为 ,过点 向垂直中心线 引垂线,垂足为点 .通过测量可得 、 、 的长度,利用测量所得的数据计算 的三角函数值,进而可求 的大小.下列关系式正确的是

| A. |
|
B. |
|
C. |
|
D. |
|
如图,在 中, 是对角线 、 的交点, , ,垂足分别为点 、 .
(1)求证: .
(2)若 , ,求 的值.
试题篮
()