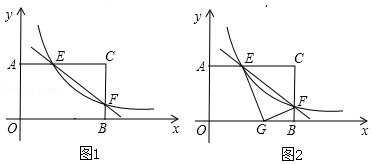
矩形 中, , .分别以 , 所在直线为 轴, 轴,建立如图1所示的平面直角坐标系. 是 边上一个动点(不与 , 重合),过点 的反比例函数 的图象与边 交于点 .
(1)当点 运动到边 的中点时,求点 的坐标;
(2)连接 ,求 的正切值;
(3)如图2,将 沿 折叠,点 恰好落在边 上的点 处,求此时反比例函数的解析式.
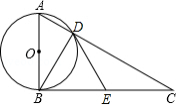
如图,已知在 中, ,以 为直径的 与 交于点 ,点 是 的中点,连接 , .
(1)若 ,求 ;
(2)求证: 是 的切线.
如图,已知AB是⊙O的直径,⊙O经过 的直角边DC上的点F,交AC边于点E,点F是弧EB的中点, ,连接AF.
(1)求证:直线CD是⊙O切线.
(2)若 , ,求 的值.

如图,在 中, , 和 关于直线 对称,连接 ,与 相交于点 ,过点 作 ,垂足为 , 相交于点 ,若 , ,则 的值为

| A. |
|
B. |
|
C. |
|
D. |
|
问题探究:
小红遇到这样一个问题:如图1, 中, , , 是中线,求 的取值范围.她的做法是:延长 到 ,使 ,连接 ,证明 ,经过推理和计算使问题得到解决.
请回答:(1)小红证明 的判定定理是: ;
(2) 的取值范围是 ;
方法运用:
(3)如图2, 是 的中线,在 上取一点 ,连结 并延长交 于点 ,使 ,求证: .
(4)如图3,在矩形 中, ,在 上取一点 ,以 为斜边作 ,且 ,点 是 的中点,连接 , ,求证: .

如图,在4×4的正方形方格图形中,小正方形的顶点称为格点,△ABC的顶点都在格点上,则图中∠ABC的余弦值是( )

A.2B. C. D.
如图,在△ ABC中,∠ CAB=55°,∠ ABC=25°,在同一平面内,将△ ABC绕 A点逆时针旋转70°得到△ ADE,连接 EC,则tan∠ DEC的值是 .

试题篮
()