初中数学中心投影试题

如图，是由一些大小相同的小正方体组合成的简单几何体．

（1）图中有      块小正方体；
（2）该几何体的主视图如图所示，请在下面方格纸中分别画出它的左视图和俯视图．

如图1是一种包装盒的表面展开图，将它围起来可得到一个几何体的模型．

（1）这个几何体模型的名称是     ．
（2）如图2是根据a，b，h的取值画出的几何体的主视图和俯视图（图中实线表示的长方形），请在网格中画出该几何体的左视图．
（3）若h=a+b，且a，b满足a²+b²﹣a﹣6b+10=0，求该几何体的表面积．

如图是由一些相同的小正方体构成的立体图形的三种视图，则构成这个立体图形的小正方体的个数是（ ）

A．6

B．7

C．9

D．8

如图是由10个同样大小的棱长为1cm的小正方体搭成的几何体．

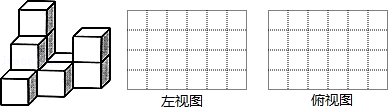
（1）该图形的体积是      cm³
（2）请在右侧的方格纸中分别画出它的左视图和俯视图．

桌上摆着一个由若干个相同正方体组成的几何体，其主视图和左视图如图所示，这个几何体最多可以由         个这样的正方体组成．

已知，如图，AB、DE是直立在地面上的两根立柱．AB=5m，某一时刻AB在阳光下的投影BC=3m．

（1）请你在图中画出此时DE在阳光下的投影EF．
（2）在测量AB的投影时，同时测量出DE在阳光下的投影长为6m，请你计算DE的长．

如图，身高1．6米的学生小李想测量学校的旗杆的高度，当他站在C处时，他头顶端的影子正好与旗杆顶端的影子重合，并测得AC=2米，BC=8米，则旗杆的高度是（ ）．

A．6．4米

B．7米

C．8米

D．9米

下图是由几个小立方块所搭几何体的俯视图，小正方形中的数字表示在该位置小立方块的个数，请画出这个几何体的主视图和左视图．

一个几何体如图所示，则该几何体的三视图正确的是（ ）．

A．	B．
C．	D．

如图1是一种包装盒的表面展开图，将它围起来可得到一个几何体的模型．

（1）这个几何体模型的名称是      ．
（2）如图2是根据a，b，h的取值画出的几何体的主视图和俯视图（图中实线表示的长方形），请在网格中画出该几何体的左视图．
（3）若h=a+b，且a，b满足a²+b²﹣a﹣6b+10=0，求该几何体的表面积．

如图，是小亮晚上在广场散步的示意图，图中线段AB表示站立在广场上的小亮，线段PO表示直立在广场上的灯杆，点P表示照明灯的位置．

（1）请你在图中画出小亮在AB处的影子；
（2）当小亮离开灯杆的距离OB=4.2cm时，身高（AB）为1.6m的小亮的影长为1.6m，问当小亮离开灯杆的距离OD=6m时，小亮的影长是多少m？

如图表示一个由相同小立方块搭成的几何体的从上面看到的形状图俯视图，小正方形中的数字表示该位置上小立方块的个数，那么该几何体的从正面看到的形状为（     ）    

下列几何体中，主视图是矩形，俯视图是圆的几何体是（ ）
 

如图，在一面与地面垂直的围墙的同侧有一根高10米的旗杆AB和一根高度未知的电线杆CD，它们都与地面垂直，为了测得电线杆的高度，一个小组的同学进行了如下测量：某一时刻，在太阳光照射下，旗杆落在围墙上的影子EF的长度为2米，落在地面上的影子BF的长为10米，而电线杆落在围墙上的影子GH的长度为3米，落在地面上的影子DH的长为5米，依据这些数据，该小组的同学计算出了电线杆的高度．

（1）该小组的同学在这里利用的是           投影的有关知识进行计算的；
（2）试计算出电线杆的高度，并写出计算的过程．

在桌上摆有一些大小相同的正方体木块，其从正面和从左面看到的形状图如图所示，则摆出这样的图形至少需要      块正方体木块，至多需要        块正方体木块．