初中数学统计表解答题

2021年是中国共产党建党100周年，某校开展了全校教师学习党史活动并进行了党史知识竞赛，从七、八年级中各随机抽取了20名教师，统计这部分教师的竞赛成绩（竞赛成绩均为整数，满分为10分，9分及以上为优秀）．相关数据统计、整理如下：

抽取七年级教师的竞赛成绩（单位：分） $:$

6，7，7，8，8，8，8，8，8，8，8，9，9，9，9，10，10，10，10，10．

七八年级教师竞赛成绩统计表

年级	七年级	八年级
平均数	8.5	8.5
中位数	$a$	9
众数	8	$b$
优秀率	$45\%$	$55\%$

根据以上信息，解答下列问题：

（1）填空： $a=$ 　　， $b=$ 　　；

（2）估计该校七年级120名教师中竞赛成绩达到8分及以上的人数；

（3）根据以上数据分析，从一个方面评价两个年级教师学习党史的竞赛成绩谁更优异．

"惜餐为荣，殄物为耻"，为了解落实"光盘行动"的情况，某校数学兴趣小组的同学调研了七、八年级部分班级某一天的餐厨垃圾质量．从七、八年级中各随机抽取10个班的餐厨垃圾质量的数据（单位： $\mathit{kg})$ ，进行整理和分析（餐厨垃圾质量用 $x$ 表示，共分为四个等级： $A$ ． $x<1$ ， $B.1⩽x<1.5$ ， $C.1.5⩽x<2$ ， $D$ ． $x⩾2)$ ，下面给出了部分信息．

七年级10个班的餐厨垃圾质量：0.8，0.8，0.8，0.9，1.1，1.1，1.6，1.7，1.9，2.3．

八年级10个班的餐厨垃圾质量中 $B$ 等级包含的所有数据为：1.0，1.0，1.0，1.0，1.2．

七、八年级抽取的班级餐厨垃圾质量统计表

年级	平均数	中位数	众数	方差	$A$ 等级所占百分比
七年级	1.3	1.1	$a$	0.26	$40\%$
八年级	1.3	$b$	1.0	0.23	$m\%$

根据以上信息，解答下列问题：

（1）直接写出上述表中 $a$ ， $b$ ， $m$ 的值；

（2）该校八年级共30个班，估计八年级这一天餐厨垃圾质量符合 $A$ 等级的班级数；

（3）根据以上数据，你认为该校七、八年级的"光盘行动"，哪个年级落实得更好？请说明理由（写出一条理由即可）．

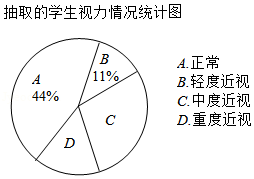
在创建"浙江省健康促进学校"的过程中，某数学兴趣小组针对视力情况随机抽取本校部分学生进行调查，并按照国家分类标准统计人数，绘制成两幅不完整的统计图表，请根据图表信息解答下列问题：

抽取的学生视力情况统计表

类别	检查结果	人数
$A$	正常	88
$B$	轻度近视	▲
$C$	中度近视	59
$D$	重度近视	▲

（1）求所抽取的学生总人数；

（2）该校共有学生约1800人，请估算该校学生中，近视程度为中度和重度的总人数；

（3）请结合上述统计数据，为该校做好近视防控，促进学生健康发展提出一条合理的建议．

为了更好地了解党的历史，宣传党的知识，传颂英雄事迹，某校团支部组建了： $A$ ．党史宣讲； $B$ ．歌曲演唱； $C$ ．校刊编撰； $D$ ．诗歌创作等四个小组，团支部将各组人数情况制成了统计图表（不完整）．

各组参加人数情况统计表

小组类别	$A$	$B$	$C$	$D$
人数（人     $)$	10	$a$	15	5

根据统计图表中的信息，解答下列问题：

（1）求 $a$ 和 $m$ 的值；

（2）求扇形统计图中 $D$ 所对应的圆心角度数；

（3）若在某一周各小组平均每人参与活动的时间如下表所示：

小组类别	$A$	$B$	$C$	$D$
平均用时（小时）	2.5	3	2	3

求这一周四个小组所有成员平均每人参与活动的时间．

某市体育中考自选项目有乒乓球、篮球和羽毛球，每个考生任选一项作为自选考试项目．

（1）求考生小红和小强自选项目相同的概率；

（2）除自选项目之外，长跑和掷实心球为必考项目．小红和小强的体育中考各项成绩（百分制）的统计图表如下：

考生	自选项目	长跑	掷实心球
小红	95	90	95
小强	90	95	95

①补全条形统计图．

②如果体育中考按自选项目占 $50\%$、长跑占 $30\%$、掷实心球占 $20\%$计算成绩（百分制），分别计算小红和小强的体育中考成绩．

为有效推进儿童青少年近视防控工作，教育部办公厅等十五部门联合制定《儿童青少年近视防控光明行动工作方案 $(2021-2025$年）》，共提出八项主要任务，其中第三项任务为强化户外活动和体育锻炼．我市各校积极落实方案精神，某学校决定开设以下四种球类的户外体育选修课程：篮球、足球、排球、乒乓球．为了解学生需求，该校随机对本校部分学生进行了“你选择哪种球类课程”的调查（要求必须选择且只能选择其中一门课程），并根据调查结果绘制成不完整的统计图表．

课程	人数
篮球	$m$
足球	21
排球	30
乒乓球	$n$

根据图表信息，解答下列问题：

（1）分别求出表中 $m$， $n$的值；

（2）求扇形统计图中“足球”对应的扇形圆心角的度数；

（3）该校共有2000名学生，请你估计其中选择“乒乓球”课程的学生人数．

为了庆祝中国共产党建党100周年，某校开展了学党史知识竞赛．参加知识竞赛的学生分为甲乙两组，每组学生均为20名，赛后根据竞赛成绩得到尚不完整的统计图表（如图），已知竞赛成绩满分为100分，统计表中 $a$， $b$满足 $b=2a$．请根据所给信息，解答下列问题：

甲组20名学生竞赛成绩统计表

成绩（分 $)$	70	80	90	100
人数	3	$a$	$b$	5

（1）求统计表中 $a$， $b$的值；

（2）小明按以下方法计算甲组20名学生竞赛成绩的平均分是： $(70+80+90+100)÷4=85$（分 $)$．根据所学统计知识判断小明的计算是否正确，若不正确，请写出正确的算式并计算出结果；

（3）如果依据平均成绩确定竞赛结果，那么竞赛成绩较好的是哪个组？请说明理由．

为了庆祝中国共产党建党100周年，某校开展了学党史知识竞赛．参加知识竞赛的学生分为甲乙两组，每组学生均为20名，赛后根据竞赛成绩得到尚不完整的统计图表（如图），已知竞赛成绩满分为100分，统计表中 $a$， $b$满足 $b=2a$．请根据所给信息，解答下列问题：

甲组20名学生竞赛成绩统计表

成绩（分 $)$	70	80	90	100
人数	3	$a$	$b$	5

（1）求统计表中 $a$， $b$的值；

（2）小明按以下方法计算甲组20名学生竞赛成绩的平均分是： $(70+80+90+100)÷4=85$（分 $)$．根据所学统计知识判断小明的计算是否正确，若不正确，请写出正确的算式并计算出结果；

（3）如果依据平均成绩确定竞赛结果，那么竞赛成绩较好的是哪个组？请说明理由．

某学校九年级有12个班，每班50名学生，为了调查该校九年级学生平均每天的睡眠时间，准备从12个班里抽取50名学生作为一个样本进行分析，并规定如下：设每个学生平均每天的睡眠时间为 $t$（单位，小时），将收集到的学生平均每天睡眠时间按 $t⩽6$、 $6<t<8$、 $t⩾8$分为三类进行分析．

（1）下列抽取方法具有代表性的是 　　．

$A$．随机抽取一个班的学生

$B$．从12个班中，随机抽取50名学生

$C$．随机抽取50名男生

$D$．随机抽取50名女生

（2）由上述具有代表性的抽取方法抽取50名学生，平均每天的睡眠时间数据如表：

睡眠时间 $t$（小时）	5	5.5	6	6.5	7	7.5	8	8.5
人数（人 $)$	1	1	2	10	15	9	10	2

①这组数据的众数和中位数分别是 　　，　　；

②估计九年级学生平均每天睡眼时间 $t⩾8$的人数大约为多少；

（3）从样本中学生平均每天眠时间 $t⩽6$的4个学生里，随机抽取2人，画树状图或列表，求抽得2人平均每天睡眠时间都是6小时的概率．

为推进扬州市"青少年茁壮成长工程"，某校开展"每日健身操"活动，为了解学生对"每日健身操"活动的喜欢程度，随机抽取了部分学生进行调查，将调查信息结果绘制成如下尚不完整的统计图表：

抽样调查各类喜欢程度人数统计表

喜欢程度	人数
$A$ ．非常喜欢	50人
$B$ ．比较喜欢	$m$ 人
$C$ ．无所谓	$n$ 人
$D$ ．不喜欢	16人

根据以上信息，回答下列问题：

（1）本次调查的样本容量是 　　；

（2）扇形统计图中表示 $A$ 程度的扇形圆心角为 　　 $°$ ，统计表中 $m=$ 　　；

（3）根据抽样调查的结果，请你估计该校2000名学生中大约有多少名学生喜欢"每日健身操"活动（包含非常喜欢和比较喜欢）．

为了防控新冠疫情，某地区积极推广疫苗接种工作，卫生防疫部门对该地区八周以来的相关数据进行收集整理，绘制得到图表：

该地区每周接种疫苗人数统计表

周次	第1周	第2周	第3周	第4周	第5周	第6周	第7周	第8周
接种人数（万人）	7	10	12	18	25	29	37	42

根据统计表中的数据，建立以周次为横坐标，接种人数为纵坐标的平面直角坐标系，并根据以上统计表中的数据描出对应的点，发现从第3周开始这些点大致分布在一条直线附近，现过其中两点 $(3,12)$、 $(8,42)$作一条直线（如图所示，该直线的函数表达式为 $y=6x-6)$，那么这条直线可近似反映该地区接种人数的变化趋势．

请根据以上信息，解答下列问题：

（1）这八周中每周接种人数的平均数为 　　万人；该地区的总人口约为 　　万人；

（2）若从第9周开始，每周的接种人数仍符合上述变化趋势．

①估计第9周的接种人数约为 　　万人；

②专家表示：疫苗接种率至少达 $60\%$，才能实现全民免疫．那么，从推广疫苗接种工作开始，最早到第几周，该地区可达到实现全民免疫的标准？

（3）实际上，受疫苗供应等客观因素，从第9周开始接种人数将会逐周减少 $a(a>0)$万人，为了尽快提高接种率，一旦周接种人数低于20万人时，卫生防疫部门将会采取措施，使得之后每周的接种能力一直维持在20万人．如果 $a=1.8$，那么该地区的建议接种人群最早将于第几周全部完成接种？

某市在实施居民用水定额管理前，对居民生活用水情况进行了调查．通过简单随机抽样，获得了100个家庭去年的月均用水量数据，将这组数据按从小到大的顺序排列，其中部分数据如表：

序号	1	2	$\dots$	25	26	$\dots$	50	51	$\dots$	75	76	$\dots$	99	100
月均用水量 $/t$	1.3	1.3	$\dots$	4.5	4.5	$\dots$	6.4	6.8	$\dots$	11	13	$\dots$	25.6	28

（1）求这组数据的中位数．已知这组数据的平均数为 $9.2t$，你对它与中位数的差异有什么看法？

（2）为了鼓励节约用水，要确定一个用水量的标准，超出这个标准的部分按1.5倍价格收费．若要使 $75\%$的家庭水费支出不受影响，你觉得这个标准应该定为多少？

2020年我国是全球主要经济体中唯一实现经济正增长的国家，各行各业蓬勃发展，其中快递业务保持着较快的增长．给出了快递业务的有关数据信息．

$2016-2017$ 年快递业务量增长速度统计表

年龄	2016	2017	2018	2019	2020
增长速度	$51.4\%$	$28.0\%$	$26.6\%$	$25.3\%$	$31.2\%$

说明：增长速度计算办法为：增长速度 $=\frac{\mathit{本年业务量}-\mathit{去年业务量}}{\mathit{去年业务量}}\times 100\%$

根据图中信息，解答下列问题：

（1） $2016-2020$ 年快递业务量最多年份的业务量是 　　亿件．

（2） $2016-2020$ 年快递业务量增长速度的中位数是 　　．

（3）下列推断合理的是 　　（填序号）．

①因为 $2016-2019$ 年快递业务量的增长速度逐年下降，所以预估2021年的快递业务量应低于2020年的快递业务量；

②因为 $2016-2020$ 年快递业务量每年的增长速度均在 $25\%$ 以上．所以预估2021年快递业务量应在 $833.6\times (1+25\%)=1042$ 亿件以上．

疫苗接种初期，为更好地响应国家对符合条件的人群接种新冠疫苗的号召，某市教育部门随机抽取了该市部分七、八、九年级教师，了解教师的疫苗接种情况，得到如下统计表：

	已接种	未接种	合计
七年级	30	10	40
八年级	35	15	$a$
九年级	40	$b$	60
合计	105	$c$	150

（1）表中， $a=$　　， $b=$　　， $c=$　　；

（2）由表中数据可知，统计的教师中接种率最高的是 　　年级教师；（填“七”或“八”或“九” $)$

（3）若该市初中七、八、九年级一共约有8000名教师，根据抽样结果估计未接种的教师约有 　　人；

（4）为更好地响应号召，立德中学从最初接种的4名教师（其中七年级1名，八年级1名，九年级2名）中随机选取2名教师谈谈接种的感受，请用列表或画树状图的方法，求选中的两名教师恰好不在同一年级的概率．

2020年我国进行了第七次全国人口普查，小星要了解我省城镇及乡村人口变化情况，根据贵州省历次人口普查结果，绘制了如下的统计图表．请利用统计图表提供的信息回答下列问题：

贵州省历次人口普查城镇人口统计表

年份	1953	1961	1982	1990	2000	2010	2020
城镇人口（万人）	110	204	540	635	845	1175	2050
城镇化率	$7\%$	$12\%$	$19\%$	$20\%$	$24\%$	$a$	$53\%$

（1）这七次人口普查乡村人口数的中位数是 　　万人；

（2）城镇化率是一个国家或地区城镇人口占其总人口的百分率，是衡量城镇化水平的一个指标．根据统计图表提供的信息，我省2010年的城镇化率 $a$ 是 　　（结果精确到 $1\%)$ ；假设未来几年我省城乡总人口数与2020年相同，城镇化率要达到 $60\%$ ，则需从乡村迁入城镇的人口数量是 　　万人（结果保留整数）；

（3）根据贵州省历次人口普查统计图表，用一句话描述我省城镇化的趋势．