初中数学方差解答题

甲乙两人进行射击训练，两人分别射击12次，如图分别统计了两人的射击成绩，已知甲射击成绩的方差 $S_{甲}^2=\frac{7}{12}$，平均成绩 $\overline{x_{甲}}=8.5$．

（1）根据图上信息，估计乙射击成绩不少于9环的概率是多少？

（2）求乙射击的平均成绩的方差，并据此比较甲乙的射击“水平”．

$S^2=\frac{1}{n}[{(x_1-\bar{x})}^2+{(x_2-\bar{x})}^2\dots {(x_n-\bar{x})}^2]$．

甲、乙两名射击运动员进行射击比赛，两人在相同条件下各射击10次，射击的成绩如图所示．

根据图中信息，回答下列问题：

（1）甲的平均数是　　，乙的中位数是　　；

（2）分别计算甲、乙成绩的方差，并从计算结果来分析，你认为哪位运动员的射击成绩更稳定？

镇政府想了解对王家村进行"精准扶贫"一年来村民的经济情况，统计员小李用简单随机抽样的方法，在全村130户家庭中随机抽取20户，调查过去一年的收入（单位：万元），从而去估计全村家庭年收入情况．

已知调查得到的数据如下：

1.9，1.3，1.7，1.4，1.6，1.5，2.7，2.1，1.5，0.9，2.6，2.0，2.1，1.0，1.8，2.2，2.4，3.2，1.3，2.8

为了便于计算，小李在原数据的每个数上都减去1.5，得到下面第二组数：

0.4，﹣0.2，0.2，﹣0.1，0.1，0，1.2，0.6，0，﹣0.6，1.1，0.5，0.6，﹣0.5，0.3，0.7，0.9，1.7，﹣0.2，1.3

（1）请你用小李得到的第二组数计算这20户家庭的平均年收入，并估计全村年收入及全村家庭年收入超过1.5万元的百分比；已知某家庭过去一年的收入是1.89万元，请你用调查得到的数据的中位数推测该家庭的收入情况在全村处于什么水平？

（2）已知小李算得第二组数的方差是 S，小王依据第二组数的方差得出原数据的方差为（1.5+ S） ²，你认为小王的结果正确吗？如果不正确，直接写出你认为正确的结果．

某校举办了一次成语知识竞赛，满分10分，学生得分均为整数，成绩达到6分及6分以上为合格，达到9分或10分为优秀，这次竞赛中，甲、乙两组学生成绩分布的折线统计图和成绩统计分析表如图所示．

（1）求出下列成绩统计分析表中 a， b的值：

组别	平均分	中位数	方差	合格率	优秀率
甲组	6.8	a	3.76	90%	30%
乙组	b	7.5	1.96	80%	20%

（2）小英同学说："这次竞赛我得了7分，在我们小组中排名属中游略偏上！"观察上面表格判断，小英是甲、乙哪个组的学生；

（3）甲组同学说他们组的合格率、优秀率均高于乙组，所以他们组的成绩好于乙组．但乙组同学不同意甲组同学的说法，认为他们组的成绩要好于甲组．请你写出两条支持乙组同学观点的理由．

下表是博文学校初三•一班慧慧、聪聪两名学生入学以来10次数学检测成绩（单位：分）．

慧慧	116	124	130	126	121	127	126	122	125	123
聪聪	122	124	125	128	119	120	121	128	114	119

回答下列问题：

（1）分别求出慧慧和聪聪成绩的平均数；

（2）分别计算慧慧和聪聪两组数据的方差；

（3）根据（1）（2）你认为选谁参加全国数学竞赛更合适？并说明理由；

（4）由于初三•二班、初三•三班和初三•四班数学成绩相对薄弱，学校打算派慧慧和聪聪分别参加三个班的数学业余辅导活动，求两名学生分别在初三•二班和初三•三班的概率．

某射击队为从甲、乙两名运动员中选拔一人参加全国比赛，对他们进行了8次测试，测试成绩（单位：环）如下表：

	第一次	第二次	第三次	第四次	第五次	第六次	第七次	第八次
甲	10	8	9	8	10	9	10	8
乙	10	7	10	10	9	8	8	10

（1）根据表格中的数据，计算出甲的平均成绩是 　　环，乙的平均成绩是 　环；

（2）分别计算甲、乙两名运动员8次测试成绩的方差；

（3）根据（1）（2）计算的结果，你认为推荐谁参加全国比赛更合适，并说明理由．

甲、乙两名射击运动员在某次训练中各射击10发子弹，成绩如表：

甲	8	9	7	9	8	6	7	8	10	8
乙	6	7	9	7	9	10	8	7	7	10

且＝8，S_乙²＝1.8，根据上述信息完成下列问题：

（1）将甲运动员的折线统计图补充完整；

（2）乙运动员射击训练成绩的众数是　　，中位数是　　．

（3）求甲运动员射击成绩的平均数和方差，并判断甲、乙两人本次射击成绩的稳定性．

某校为了了解初中学生每天的睡眠时间（单位为小时），随机调查了该校的部分初中学生，根据调查结果，绘制出如图统计图．

请根据相关信息，解答下列问题：

（1）本次接受调查的初中学生人数为 　　人，扇形统计图中的 $m=$ 　　，条形统计图中的 $n=$ 　　；

（2）所调查的初中学生每天睡眠时间的众数是 　　，方差是 　　；

（3）该校共有1600名初中学生，根据样本数据，估计该校初中学生每天睡眠时间不足8小时的人数．

6月26日是"国际禁毒日"，某中学组织七、八年级全体学生开展了"禁毒知识"网上竞赛活动．为了解竞赛情况，从两个年级各随机抽取了10名同学的成绩（满分为100分），收集数据为：七年级90，95，95，80，90，80，85，90，85，100；八年级85，85，95，80，95，90，90，90，100，90．

整理数据：

分数 人数 年级	80	85	90	95	100
七年级	2	2	3	2	1
八年级	1	2	4	$a$	1

解析数据：

	平均数	中位数	众数	方差
七年级	89	$b$	90	39
八年级	$c$	90	$d$	30

根据以上信息回答下列问题：

（1）请直接写出表格中 $a$ ， $b$ ， $c$ ， $d$ 的值；

（2）通过数据解析，你认为哪个年级的成绩比较好？请说明理由；

（3）该校七、八年级共有600人，本次竞赛成绩不低于90分的为"优秀"．估计这两个年级共有多少名学生达到"优秀"？

某射箭队准备从王方、李明二人中选拔1人参加射箭比赛，在选拔赛中，两人各射箭10次的成绩（单位：环数）如下：

次数	1	2	3	4	5	6	7	8	9	10
王方	7	10	9	8	6	9	9	7	10	10
李明	8	9	8	9	8	8	9	8	10	8

（1）根据以上数据，将下面两个表格补充完整：

王方10次射箭得分情况

环数	6	7	8	9	10
频数
频率

李明10次射箭得分情况

环数	6	7	8	9	10
频数
频率

（2）分别求出两人10次射箭得分的平均数；

（3）从两人成绩的稳定性角度分析，应选派谁参加比赛合适．

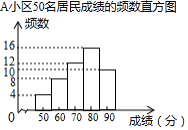
在“创全国文明城市”活动中，某社区为了了解居民掌握垃圾分类知识的情况进行调查．其中、两小区分别有500名居民，社区从中各随机抽取50名居民进行相关知识测试，并将成绩进行整理得到部分信息：

[信息一]小区50名居民成绩的频数直方图如图（每一组含前一个边界值，不含后一个边界值）；

[信息二]图中，从左往右第四组的成绩如下

75	75	79	79	79	79	80	80
81	82	82	83	83	84	84	84

[信息三]、两小区各50名居民成绩的平均数、中位数、众数、优秀率分及以上为优秀）、方差等数据如下（部分空缺）

小区	平均数	中位数	众数	优秀率	方差
	75.1		79		277
	75.1	77	76		211

根据以上信息，回答下列问题：

（1）求小区50名居民成绩的中位数．

（2）请估计小区500名居民中能超过平均数的有多少人？

（3）请尽量从多个角度比较、分析，两小区居民掌握垃圾分类知识的情况．

在推进嘉兴市城乡生活垃圾分类的行动中，某社区为了了解居民掌握垃圾分类知识的情况进行调查．其中、两小区分别有500名居民参加了测试，社区从中各随机抽取50名居民成绩进行整理得到部分信息：

[信息一]小区50名居民成绩的频数直方图如图（每一组含前一个边界值，不含后一个边界值）

[信息二]上图中，从左往右第四组的成绩如下：

75	75	79	79	79	79	80	80
81	82	82	83	83	84	84	84

[信息三]、两小区各50名居民成绩的平均数、中位数、众数、优秀率分及以上为优秀）、方差等数据如下（部分空缺）

小区	平均数	中位数	众数	优秀率	方差
	75.1	75	79		277
	75.1	77	76		211

根据以上信息，回答下列问题：

（1）求小区50名居民成绩的中位数．

（2）请估计小区500名居民成绩能超过平均数的人数．

（3）请尽量从多个角度，选择合适的统计量分析，两小区参加测试的居民掌握垃圾分类知识的情况．

称量五筐水果的质量，若每筐以50千克为基准，超过基准部分的千克数记为正数，不足基准部分的千克数记为负数，甲组为实际称量读数，乙组为记录数据，并把所得数据整理成如下统计表和未完成的统计图（单位：千克）．

实际称量读数和记录数据统计表

序号 数据	1	2	3	4	5
甲组	48	52	47	49	54
乙组		2			4

（1）补充完成乙组数据的折线统计图．

（2）①甲，乙两组数据的平均数分别为，，写出与之间的等量关系．

②甲，乙两组数据的方差分别为，，比较与的大小，并说明理由．

某校为了解七、八年级学生英语听力训练情况（七、八年级学生人数相同），某周从这两个年级学生中分别随机抽查了30名同学，调查了他们周一至周五的听力训练情况，根据调查情况得到如下统计图表：

周一至周五英语听力训练人数统计表

年级	参加英语听力训练人数
	周一	周二	周三	周四	周五
七年级	15	20		30	30
八年级	20	24	26	30	30
合计	35	44	51	60	60

（1）填空：　　；

（2）根据上述统计图表完成下表中的相关统计量：

年级	平均训练时间的中位数	参加英语听力训练人数的方差
七年级	24	34
八年级		14.4

（3）请你利用上述统计图表对七、八年级英语听力训练情况写出两条合理的评价；

（4）请你结合周一至周五英语听力训练人数统计表，估计该校七、八年级共480名学生中周一至周五平均每天有多少人进行英语听力训练．

为了调查甲、乙两台包装机分装标准质量为奶粉的情况，质检员进行了抽样调查，过程如下，请补全表一、表二中的空白，并回答提出的问题．

收集数据：

从甲、乙包装机分装的奶粉中各自随机抽取10袋，测得实际质量（单位：如下：

甲：400，400，408，406，410，409，400，393，394，395

乙：403，404，396，399，402，402，405，397，402，398

整理数据：

表一

质量 频数 种类
甲	3	0	3	0	1	3
乙	0		1	5		0

分析数据：

表二

种类	平均数	中位数	众数	方差
甲	401.5		400	36.85
乙	400.8	402		8.56

得出结论：

包装机分装情况比较好的是　　（填甲或乙），说明你的理由．