初中数学方差解答题

"惜餐为荣，殄物为耻"，为了解落实"光盘行动"的情况，某校数学兴趣小组的同学调研了七、八年级部分班级某一天的餐厨垃圾质量．从七、八年级中各随机抽取10个班的餐厨垃圾质量的数据（单位： $\mathit{kg})$ ，进行整理和分析（餐厨垃圾质量用 $x$ 表示，共分为四个等级： $A$ ． $x<1$ ， $B.1⩽x<1.5$ ， $C.1.5⩽x<2$ ， $D$ ． $x⩾2)$ ，下面给出了部分信息．

七年级10个班的餐厨垃圾质量：0.8，0.8，0.8，0.9，1.1，1.1，1.6，1.7，1.9，2.3．

八年级10个班的餐厨垃圾质量中 $B$ 等级包含的所有数据为：1.0，1.0，1.0，1.0，1.2．

七、八年级抽取的班级餐厨垃圾质量统计表

年级	平均数	中位数	众数	方差	$A$ 等级所占百分比
七年级	1.3	1.1	$a$	0.26	$40\%$
八年级	1.3	$b$	1.0	0.23	$m\%$

根据以上信息，解答下列问题：

（1）直接写出上述表中 $a$ ， $b$ ， $m$ 的值；

（2）该校八年级共30个班，估计八年级这一天餐厨垃圾质量符合 $A$ 等级的班级数；

（3）根据以上数据，你认为该校七、八年级的"光盘行动"，哪个年级落实得更好？请说明理由（写出一条理由即可）．

小聪、小明准备代表班级参加学校"党史知识"竞赛，班主任对这两名同学测试了6次，获得如图测试成绩折线统计图．根据图中信息，解答下列问题：

（1）要评价每位同学成绩的平均水平，你选择什么统计量？求这个统计量．

（2）求小聪成绩的方差．

（3）现求得小明成绩的方差为 $S_{\mathit{小明}}^2=3$ （单位：平方分）．根据折线统计图及上面两小题的计算，你认为哪位同学的成绩较好？请简述理由．

2021年是中国共产党成立100周年．为普及党史知识，培养爱国主义精神，今年五月份，某市党校举行党史知识竞赛，每个班级各选派15名学员参加了网上测试，现对甲、乙两班学员的分数进行整理分析如下：

甲班15名学员测试成绩（满分100分）统计如下：

87，84，88，76，93，87，73，98，86，87，79，85，84，85，98．

乙班15名学员测试成绩（满分100分）统计如下：

77，88，92，85，76，90，76，91，88，81，85，88，98，86，89

（1）按如表分数段整理两班测试成绩

班级	$70.5~75.5$	$75.5~80.5$	$80.5~85.5$	$85.5~90.5$	$90.5~95.5$	$95.5~100.5$
甲	1	2	$a$	5	1	2
乙	0	3	3	6	2	1

表中 $a=$　　；

（2）补全甲班15名学员测试成绩的频数分布直方图；

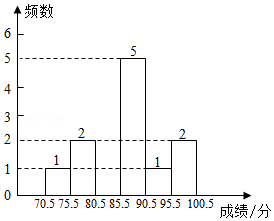
（3）两班测试成绩的平均数、众数、中位数、方差如表所示：

班级	平均数	众数	中位数	方差
甲	86	$x$	86	44.8
乙	86	88	$y$	36.7

表中 $x=$　　， $y=$　　．

（4）以上两个班级学员掌握党史相关知识的整体水平较好的是 　　班；

（5）本次测试两班的最高分都是98分，其中甲班2人，乙班1人．现从以上三人中随机抽取两人代表党校参加全市党史知识竞赛，根据树状图或表格求出恰好抽取甲、乙两班各一人参加全市党史知识竞赛的概率．

为了提高农副产品的国际竞争力，我国一些行业协会对农副产品的规格进行了划分．某外贸公司要出口一批规格为 $75g$的鸡腿，现有两个厂家提供货源，它们的价格相同，鸡腿的品质相近质检员分别从两厂的产品中抽样调查了20只鸡腿，它们的质量（单位： $g)$如下：

甲厂：76，74，74，76，73，76，76，77，78，74，76，70，76，76，73，70，77，79，78，71；

乙厂：75，76，77，77，78，77，76，71，74，75，79，71，72，74，73，74，70，79，75，77．

甲厂鸡腿质量频数统计表

质量 $x\left(g\right)$	频数	频率
$68⩽x<71$	2	0.1
$71⩽x<74$	3	0.15
$74⩽x<77$	10	$a$
$77⩽x<80$	5	0.25
合计	20	1

分析上述数据，得到下表：

统计量 厂家	平均数	中位数	众数	方差
甲厂	75	76	$b$	6.3
乙厂	75	75	77	6.6

请你根据图表中的信息完成下列问题：

（1） $a=$　　， $b=$　　；

（2）补全频数分布直方图；

（3）如果只考虑出口鸡腿规格，请结合表中的某个统计量，为外贸公司选购鸡腿提供参考建议；

（4）某外贸公司从甲厂采购了20000只鸡腿，并将质量（单位： $g)$在 $71⩽x<77$的鸡腿加工成优等品，请估计可以加工成优等品的鸡腿有多少只？

为庆祝中国共产党建党100周年，某校举行了“红色华诞，党旗飘扬”党史知识竞赛．为了解竞赛成绩，抽样调查了七、八年级部分学生的分数，过程如下：

（1）收集数据．

从该校七、八年级学生中各随机抽取20名学生的分数，其中八年级的分数如下：

81 83 84 85 86 87 87 88 89 90

92 92 93 95 95 95 99 99 100 100

（2）整理、描述数据．

按下表分段整理描述样本数据：

分数 $x$ 人数 年级	$80⩽x<85$	$85⩽x<90$	$90⩽x<95$	$95⩽x⩽100$
七年级	4	6	2	8
八年级	3	$a$	4	7

（3）分析数据．

两组样本数据的平均数中位数、众数、方差如表所示：

年级	平均数	中位数	众数	方差
七年级	91	89	97	40.9
八年级	91	$b$	$c$	33.2

根据以上提供的信息，解答下列问题：

①填空： $a=$　　， $b=$　　， $c=$　　；

②样本数据中，七年级甲同学和八年级乙同学的分数都为90分，　　同学的分数在本年级抽取的分数中从高到低排序更靠前（填“甲”或“乙” $)$；

③从样本数据分析来看，分数较整齐的是 　　年级（填“七”或“八” $)$；

④如果七年级共有400人参赛，则该年级约有 　　人的分数不低于95分．

九（1）班准备从甲、乙两名男生中选派一名参加学校组织的一分钟跳绳比赛，在相同的条件下，分别对两名男生进行了八次一分钟跳绳测试．现将测试结果绘制成如下不完整的统计图表，请根据统计图表中的信息解答下列问题：

	平均数	中位数	众数	方差
甲	175	$a$	$b$	93.75
乙	175	175	180，175，170	$c$

（1）求 $a$、 $b$的值；

（2）若九（1）班选一位成绩稳定的选手参赛，你认为应选谁，请说明理由；

（3）根据以上的数据分析，请你运用所学统计知识，任选两个角度评价甲乙两名男生一分钟跳绳成绩谁优．

某校要从甲，乙两名学生中挑选一名学生参加数学竞赛，在最近的8次选拔赛中，他们的成绩（成绩均为整数，单位：分）如下：

甲：92，95，96，88，92，98，99，100

乙：100，87，92，93，9■，95，97，98

由于保存不当，学生乙有一次成绩的个位数字模糊不清，

（1）求甲成绩的平均数和中位数；

（2）求事件“甲成绩的平均数大于乙成绩的平均数”的概率；

（3）当甲成绩的平均数与乙成绩的平均数相等时，请用方差大小说明应选哪个学生参加数学竞赛．

$A$， $B$两家酒店规模相当，去年下半年的月盈利折线统计图如图所示．

（1）要评价这两家酒店 $7~12$月的月盈利的平均水平，你选择什么统计量？求出这个统计量．

（2）已知 $A$， $B$两家酒店 $7~12$月的月盈利的方差分别为1.073（平方万元），0.54（平方万元）．根据所给的方差和你在（1）中所求的统计量，结合折线统计图，你认为去年下半年哪家酒店经营状况较好？请简述理由．

某厂为了检验甲、乙两车间生产的同一款新产品的合格情况（尺寸范围为 $176\mathit{mm}~185\mathit{mm}$的产品为合格），随机各抽取了20个样品进行检测，过程如下：

收集数据（单位： $\mathit{mm})$

甲车间：168，175，180，185，172，189，185，182，185，174，192，180，185，178，173，185，169，187，176，180．

乙车间：186，180，189，183，176，173，178，167，180，175，178，182，180，179，185，180，184，182，180，183．

整理数据：

	$165.5~170.5$	$170.5~175.5$	$175.5~180.5$	$180.5~185.5$	$185.5~190.5$	$190.5~195.5$
甲车间	2	4	5	6	2	1
乙车间	1	2	$a$	$b$	2	0

分析数据：

车间	平均数	众数	中位数	方差
甲车间	180	185	180	43.1
乙车间	180	180	180	22.6

应用数据：

（1）计算甲车间样品的合格率．

（2）估计乙车间生产的1000个该款新产品中合格产品有多少个？

（3）结合上述数据信息，请判断哪个车间生产的新产品更好，并说明理由．

为助力新冠肺炎疫情后经济的复苏，天天快餐公司积极投入到复工复产中．现有 $A$、 $B$两家农副产品加工厂到该公司推销鸡腿，两家鸡腿的价格相同，品质相近．该公司决定通过检查质量来确定选购哪家的鸡腿．检察人员从两家分别抽取100个鸡腿，然后再从中随机各抽取10个，记录它们的质量（单位：克）如表：

$A$加工厂	74	75	75	75	73	77	78	72	76	75
$B$加工厂	78	74	78	73	74	75	74	74	75	75

（1）根据表中数据，求 $A$加工厂的10个鸡腿质量的中位数、众数、平均数；

（2）估计 $B$加工厂这100个鸡腿中，质量为75克的鸡腿有多少个？

（3）根据鸡腿质量的稳定性，该快餐公司应选购哪家加工厂的鸡腿？

8年级某老师对一、二班学生阅读水平进行测试，并将成绩进行了统计，绘制了如下图表（得分为整数，满分为10分，成绩大于或等于6分为合格，成绩大于或等于9分为优秀）．

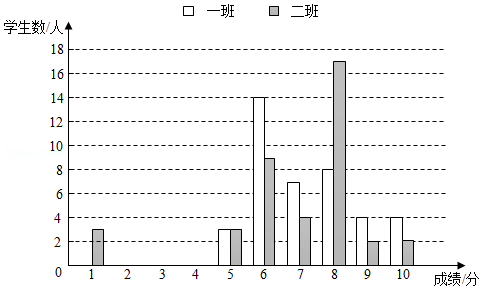
	平均分	方差	中位数	众数	合格率	优秀率
一班	7.2	2.11	7	6	$92.5\%$	$20\%$
二班	6.85	4.28	8	8	$85\%$	$10\%$

根据图表信息，回答问题：

（1）用方差推断，　   　班的成绩波动较大；用优秀率和合格率推断，　 　班的阅读水平更好些；

（2）甲同学用平均分推断，一班阅读水平更好些；乙同学用中位数或众数推断，二班阅读水平更好些．你认为谁的推断比较科学合理，更客观些．为什么？

如图是某市连续5天的天气情况．

（1）利用方差判断该市这5天的日最高气温波动大还是日最低气温波动大；

（2）根据如图提供的信息，请再写出两个不同类型的结论．

甲、乙两城市某月1日 $~10$日中午12时的气温（单位： ${}^{°}\text{C})$如下：

甲 22 20 25 22 18 23 13 27 27 22

乙 21 22 24 18 28 21 18 19 26 18

整理数据：这两组数据的频数分布表如表一．

分析数据：这两组数据的平均数、中位数、众数和方差如表二所示．

表一

分组	频数
	甲	乙
$10⩽x<15$	1	0
$15⩽x<20$	1	$a$
$20⩽x<25$	5	$b$
$25⩽x<30$	3	2

表二

统计量	甲	乙
平均数	$c$	21.5
中位数	22	$d$
众数	22	$e$
方差	16.09	11.25

请填空：

（1）在上表中， $a=$　　， $b=$　　， $c=$　　， $d=$　　， $e=$　　；

（2）　　城的气温变化较小；

（3）　　城的气温较高，理由是　　．

为了发展学生的核心素养，培养学生的综合能力，某中学利用“阳光大课间”，组织学生积极参加丰富多彩的课外活动，学校成立了舞蹈队、足球队、篮球队、毽子队、射击队等，其中射击队在某次训练中，甲、乙两名队员各射击10发子弹，成绩用如图的折线统计图表示：（甲为实线，乙为虚线）

（1）依据折线统计图，得到下面的表格：

射击次序（次 $)$	1	2	3	4	5	6	7	8	9	10
甲的成绩（环 $)$	8	9	7	9	8	6	7	$a$	10	8
乙的成绩（环 $)$	6	7	9	7	9	10	8	7	$b$	10

其中 $a=$　， $b=$　　；

（2）甲成绩的众数是　　环，乙成绩的中位数是　　环；

（3）请运用方差的知识，判断甲、乙两人谁的成绩更为稳定？

（4）该校射击队要参加市组织的射击比赛，已预选出2名男同学和2名女同学，现要从这4名同学中任意选取2名同学参加比赛，请用列表或画树状图法，求出恰好选到1男1女的概率．

为了考察甲、乙两种成熟期小麦的株高长势情况，现从中随机抽取6株，并测得它们的株高（单位： $\mathit{cm})$如表所示：

甲	63	66	63	61	64	61
乙	63	65	60	63	64	63

（1）请分别计算表内两组数据的方差，并借此比较哪种小麦的株高长势比较整齐？

（2）现将进行两种小麦优良品种杂交实验，需从表内的甲、乙两种小麦中，各随机抽取一株进行配对，以预估整体配对状况，请你用列表法或画树状图的方法，求所抽取的两株配对小麦株高恰好都等于各自平均株高的概率．