初中数学方差解答题

在推进嘉兴市城乡生活垃圾分类的行动中，某社区为了了解居民掌握垃圾分类知识的情况进行调查．其中、两小区分别有500名居民参加了测试，社区从中各随机抽取50名居民成绩进行整理得到部分信息：

[信息一]小区50名居民成绩的频数直方图如图（每一组含前一个边界值，不含后一个边界值）

[信息二]上图中，从左往右第四组的成绩如下：

75	75	79	79	79	79	80	80
81	82	82	83	83	84	84	84

[信息三]、两小区各50名居民成绩的平均数、中位数、众数、优秀率分及以上为优秀）、方差等数据如下（部分空缺）

小区	平均数	中位数	众数	优秀率	方差
	75.1	75	79		277
	75.1	77	76		211

根据以上信息，回答下列问题：

（1）求小区50名居民成绩的中位数．

（2）请估计小区500名居民成绩能超过平均数的人数．

（3）请尽量从多个角度，选择合适的统计量分析，两小区参加测试的居民掌握垃圾分类知识的情况．

称量五筐水果的质量，若每筐以50千克为基准，超过基准部分的千克数记为正数，不足基准部分的千克数记为负数，甲组为实际称量读数，乙组为记录数据，并把所得数据整理成如下统计表和未完成的统计图（单位：千克）．

实际称量读数和记录数据统计表

序号 数据	1	2	3	4	5
甲组	48	52	47	49	54
乙组		2			4

（1）补充完成乙组数据的折线统计图．

（2）①甲，乙两组数据的平均数分别为，，写出与之间的等量关系．

②甲，乙两组数据的方差分别为，，比较与的大小，并说明理由．

某校为了解七、八年级学生英语听力训练情况（七、八年级学生人数相同），某周从这两个年级学生中分别随机抽查了30名同学，调查了他们周一至周五的听力训练情况，根据调查情况得到如下统计图表：

周一至周五英语听力训练人数统计表

年级	参加英语听力训练人数
	周一	周二	周三	周四	周五
七年级	15	20		30	30
八年级	20	24	26	30	30
合计	35	44	51	60	60

（1）填空：　　；

（2）根据上述统计图表完成下表中的相关统计量：

年级	平均训练时间的中位数	参加英语听力训练人数的方差
七年级	24	34
八年级		14.4

（3）请你利用上述统计图表对七、八年级英语听力训练情况写出两条合理的评价；

（4）请你结合周一至周五英语听力训练人数统计表，估计该校七、八年级共480名学生中周一至周五平均每天有多少人进行英语听力训练．

为了调查甲、乙两台包装机分装标准质量为奶粉的情况，质检员进行了抽样调查，过程如下，请补全表一、表二中的空白，并回答提出的问题．

收集数据：

从甲、乙包装机分装的奶粉中各自随机抽取10袋，测得实际质量（单位：如下：

甲：400，400，408，406，410，409，400，393，394，395

乙：403，404，396，399，402，402，405，397，402，398

整理数据：

表一

质量 频数 种类
甲	3	0	3	0	1	3
乙	0		1	5		0

分析数据：

表二

种类	平均数	中位数	众数	方差
甲	401.5		400	36.85
乙	400.8	402		8.56

得出结论：

包装机分装情况比较好的是　　（填甲或乙），说明你的理由．

甲、乙、丙三位运动员在相同条件下各射靶10次，每次射靶的成绩如下：

甲：9，10，8，5，7，8，10，8，8，7

乙：5，7，8，7，8，9，7，9，10，10

丙：7，6，8，5，4，7，6，3，9，5

（1）根据以上数据完成下表：

	平均数	中位数	方差
甲	8	8
乙	8	8	2.2
丙	6		3

（2）根据表中数据分析，哪位运动员的成绩最稳定，并简要说明理由；

（3）比赛时三人依次出场，顺序由抽签方式决定，求甲、乙相邻出场的概率．

小云统计了自己所住小区5月1日至30日的厨余垃圾分出量（单位：千克），相关信息如下：

．小云所住小区5月1日至30日的厨余垃圾分出量统计图：

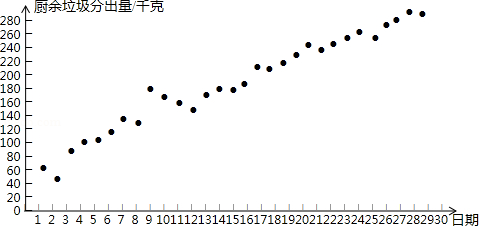
．小云所住小区5月1日至30日分时段的厨余垃圾分出量的平均数如下：

时段	1日至10日	11日至20日	21日至30日
平均数	100	170	250

（1）该小区5月1日至30日的厨余垃圾分出量的平均数约为　173　（结果取整数）；

（2）已知该小区4月的厨余垃圾分出量的平均数为60，则该小区5月1日至30日的厨余垃圾分出量的平均数约为4月的　　倍（结果保留小数点后一位）；

（3）记该小区5月1日至10日的厨余垃圾分出量的方差为，5月11日至20日的厨余垃圾分出量的方差为，5月21日至30日的厨余垃圾分出量的方差为．直接写出，，的大小关系．