初中数学方差解答题

下表是博文学校初三•一班慧慧、聪聪两名学生入学以来10次数学检测成绩（单位：分）．

慧慧	116	124	130	126	121	127	126	122	125	123
聪聪	122	124	125	128	119	120	121	128	114	119

回答下列问题：

（1）分别求出慧慧和聪聪成绩的平均数；

（2）分别计算慧慧和聪聪两组数据的方差；

（3）根据（1）（2）你认为选谁参加全国数学竞赛更合适？并说明理由；

（4）由于初三•二班、初三•三班和初三•四班数学成绩相对薄弱，学校打算派慧慧和聪聪分别参加三个班的数学业余辅导活动，求两名学生分别在初三•二班和初三•三班的概率．

为了发展学生的核心素养，培养学生的综合能力，某中学利用“阳光大课间”，组织学生积极参加丰富多彩的课外活动，学校成立了舞蹈队、足球队、篮球队、毽子队、射击队等，其中射击队在某次训练中，甲、乙两名队员各射击10发子弹，成绩用如图的折线统计图表示：（甲为实线，乙为虚线）

（1）依据折线统计图，得到下面的表格：

射击次序（次 $)$	1	2	3	4	5	6	7	8	9	10
甲的成绩（环 $)$	8	9	7	9	8	6	7	$a$	10	8
乙的成绩（环 $)$	6	7	9	7	9	10	8	7	$b$	10

其中 $a=$　， $b=$　　；

（2）甲成绩的众数是　　环，乙成绩的中位数是　　环；

（3）请运用方差的知识，判断甲、乙两人谁的成绩更为稳定？

（4）该校射击队要参加市组织的射击比赛，已预选出2名男同学和2名女同学，现要从这4名同学中任意选取2名同学参加比赛，请用列表或画树状图法，求出恰好选到1男1女的概率．

甲、乙两名射击运动员在某次训练中各射击10发子弹，成绩如表：

甲	8	9	7	9	8	6	7	8	10	8
乙	6	7	9	7	9	10	8	7	7	10

且＝8，S_乙²＝1.8，根据上述信息完成下列问题：

（1）将甲运动员的折线统计图补充完整；

（2）乙运动员射击训练成绩的众数是　　，中位数是　　．

（3）求甲运动员射击成绩的平均数和方差，并判断甲、乙两人本次射击成绩的稳定性．

小聪、小明准备代表班级参加学校"党史知识"竞赛，班主任对这两名同学测试了6次，获得如图测试成绩折线统计图．根据图中信息，解答下列问题：

（1）要评价每位同学成绩的平均水平，你选择什么统计量？求这个统计量．

（2）求小聪成绩的方差．

（3）现求得小明成绩的方差为 $S_{\mathit{小明}}^2=3$ （单位：平方分）．根据折线统计图及上面两小题的计算，你认为哪位同学的成绩较好？请简述理由．

6月26日是"国际禁毒日"，某中学组织七、八年级全体学生开展了"禁毒知识"网上竞赛活动．为了解竞赛情况，从两个年级各随机抽取了10名同学的成绩（满分为100分），收集数据为：七年级90，95，95，80，90，80，85，90，85，100；八年级85，85，95，80，95，90，90，90，100，90．

整理数据：

分数 人数 年级	80	85	90	95	100
七年级	2	2	3	2	1
八年级	1	2	4	$a$	1

解析数据：

	平均数	中位数	众数	方差
七年级	89	$b$	90	39
八年级	$c$	90	$d$	30

根据以上信息回答下列问题：

（1）请直接写出表格中 $a$ ， $b$ ， $c$ ， $d$ 的值；

（2）通过数据解析，你认为哪个年级的成绩比较好？请说明理由；

（3）该校七、八年级共有600人，本次竞赛成绩不低于90分的为"优秀"．估计这两个年级共有多少名学生达到"优秀"？

垫球是排球队常规训练的重要项目之一．下列图表中的数据是甲、乙、丙三人每人十次垫球测试的成绩．测试规则为连续接球10个，每垫球到位1个记1分．

                                                   运动员甲测试成绩表

测试序号	1	2	3	4	5	6	7	8	9	10
成绩（分 $)$	7	6	8	7	7	5	8	7	8	7

（1）写出运动员甲测试成绩的众数和中位数；

（2）在他们三人中选择一位垫球成绩优秀且较为稳定的接球能手作为自由人，你认为选谁更合适？为什么？（参考数据：三人成绩的方差分别为 $S_{甲}^2=0.8$、 $S_{乙}^2=0.4$、 $S_{丙}^2=0.8)$

（3）甲、乙、丙三人相互之间进行垫球练习，每个人的球都等可能的传给其他两人，球最先从甲手中传出，第三轮结束时球回到甲手中的概率是多少？（用树状图或列表法解答）

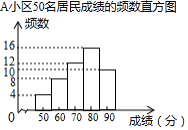
在“创全国文明城市”活动中，某社区为了了解居民掌握垃圾分类知识的情况进行调查．其中、两小区分别有500名居民，社区从中各随机抽取50名居民进行相关知识测试，并将成绩进行整理得到部分信息：

[信息一]小区50名居民成绩的频数直方图如图（每一组含前一个边界值，不含后一个边界值）；

[信息二]图中，从左往右第四组的成绩如下

75	75	79	79	79	79	80	80
81	82	82	83	83	84	84	84

[信息三]、两小区各50名居民成绩的平均数、中位数、众数、优秀率分及以上为优秀）、方差等数据如下（部分空缺）

小区	平均数	中位数	众数	优秀率	方差
	75.1		79		277
	75.1	77	76		211

根据以上信息，回答下列问题：

（1）求小区50名居民成绩的中位数．

（2）请估计小区500名居民中能超过平均数的有多少人？

（3）请尽量从多个角度比较、分析，两小区居民掌握垃圾分类知识的情况．

为助力新冠肺炎疫情后经济的复苏，天天快餐公司积极投入到复工复产中．现有 $A$、 $B$两家农副产品加工厂到该公司推销鸡腿，两家鸡腿的价格相同，品质相近．该公司决定通过检查质量来确定选购哪家的鸡腿．检察人员从两家分别抽取100个鸡腿，然后再从中随机各抽取10个，记录它们的质量（单位：克）如表：

$A$加工厂	74	75	75	75	73	77	78	72	76	75
$B$加工厂	78	74	78	73	74	75	74	74	75	75

（1）根据表中数据，求 $A$加工厂的10个鸡腿质量的中位数、众数、平均数；

（2）估计 $B$加工厂这100个鸡腿中，质量为75克的鸡腿有多少个？

（3）根据鸡腿质量的稳定性，该快餐公司应选购哪家加工厂的鸡腿？

称量五筐水果的质量，若每筐以50千克为基准，超过基准部分的千克数记为正数，不足基准部分的千克数记为负数，甲组为实际称量读数，乙组为记录数据，并把所得数据整理成如下统计表和未完成的统计图（单位：千克）．

实际称量读数和记录数据统计表

序号 数据	1	2	3	4	5
甲组	48	52	47	49	54
乙组		2			4

（1）补充完成乙组数据的折线统计图．

（2）①甲，乙两组数据的平均数分别为，，写出与之间的等量关系．

②甲，乙两组数据的方差分别为，，比较与的大小，并说明理由．

甲、乙两运动员的射击成绩（靶心为10环）统计如下表（不完全） $:$

运动员 环数 次数	1	2	3	4	5
甲	10	8	9	10	8
乙	10	9	9	$a$	$b$

某同学计算出了甲的成绩平均数是9，方差是

$S_{甲}^2=\frac{1}{5}[{(10-9)}^2+{(8-9)}^2+{(9-9)}^2+{(10-9)}^2+\left(8-9{)}^2\right]=0.8$，请作答：

（1）在图中用折线统计图将甲运动员的成绩表示出来；

（2）若甲、乙射击成绩平均数都一样，则 $a+b=$　　；

（3）在（2）的条件下，当甲比乙的成绩较稳定时，请列举出 $a$、 $b$的所有可能取值，并说明理由．

"惜餐为荣，殄物为耻"，为了解落实"光盘行动"的情况，某校数学兴趣小组的同学调研了七、八年级部分班级某一天的餐厨垃圾质量．从七、八年级中各随机抽取10个班的餐厨垃圾质量的数据（单位： $\mathit{kg})$ ，进行整理和分析（餐厨垃圾质量用 $x$ 表示，共分为四个等级： $A$ ． $x<1$ ， $B.1⩽x<1.5$ ， $C.1.5⩽x<2$ ， $D$ ． $x⩾2)$ ，下面给出了部分信息．

七年级10个班的餐厨垃圾质量：0.8，0.8，0.8，0.9，1.1，1.1，1.6，1.7，1.9，2.3．

八年级10个班的餐厨垃圾质量中 $B$ 等级包含的所有数据为：1.0，1.0，1.0，1.0，1.2．

七、八年级抽取的班级餐厨垃圾质量统计表

年级	平均数	中位数	众数	方差	$A$ 等级所占百分比
七年级	1.3	1.1	$a$	0.26	$40\%$
八年级	1.3	$b$	1.0	0.23	$m\%$

根据以上信息，解答下列问题：

（1）直接写出上述表中 $a$ ， $b$ ， $m$ 的值；

（2）该校八年级共30个班，估计八年级这一天餐厨垃圾质量符合 $A$ 等级的班级数；

（3）根据以上数据，你认为该校七、八年级的"光盘行动"，哪个年级落实得更好？请说明理由（写出一条理由即可）．

2021年是中国共产党成立100周年．为普及党史知识，培养爱国主义精神，今年五月份，某市党校举行党史知识竞赛，每个班级各选派15名学员参加了网上测试，现对甲、乙两班学员的分数进行整理分析如下：

甲班15名学员测试成绩（满分100分）统计如下：

87，84，88，76，93，87，73，98，86，87，79，85，84，85，98．

乙班15名学员测试成绩（满分100分）统计如下：

77，88，92，85，76，90，76，91，88，81，85，88，98，86，89

（1）按如表分数段整理两班测试成绩

班级	$70.5~75.5$	$75.5~80.5$	$80.5~85.5$	$85.5~90.5$	$90.5~95.5$	$95.5~100.5$
甲	1	2	$a$	5	1	2
乙	0	3	3	6	2	1

表中 $a=$　　；

（2）补全甲班15名学员测试成绩的频数分布直方图；

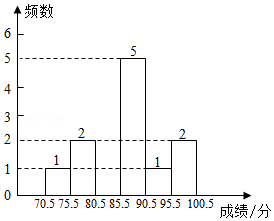
（3）两班测试成绩的平均数、众数、中位数、方差如表所示：

班级	平均数	众数	中位数	方差
甲	86	$x$	86	44.8
乙	86	88	$y$	36.7

表中 $x=$　　， $y=$　　．

（4）以上两个班级学员掌握党史相关知识的整体水平较好的是 　　班；

（5）本次测试两班的最高分都是98分，其中甲班2人，乙班1人．现从以上三人中随机抽取两人代表党校参加全市党史知识竞赛，根据树状图或表格求出恰好抽取甲、乙两班各一人参加全市党史知识竞赛的概率．

8年级某老师对一、二班学生阅读水平进行测试，并将成绩进行了统计，绘制了如下图表（得分为整数，满分为10分，成绩大于或等于6分为合格，成绩大于或等于9分为优秀）．

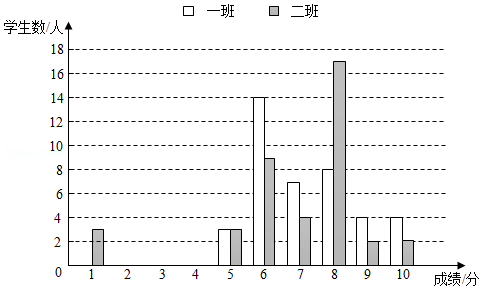
	平均分	方差	中位数	众数	合格率	优秀率
一班	7.2	2.11	7	6	$92.5\%$	$20\%$
二班	6.85	4.28	8	8	$85\%$	$10\%$

根据图表信息，回答问题：

（1）用方差推断，　   　班的成绩波动较大；用优秀率和合格率推断，　 　班的阅读水平更好些；

（2）甲同学用平均分推断，一班阅读水平更好些；乙同学用中位数或众数推断，二班阅读水平更好些．你认为谁的推断比较科学合理，更客观些．为什么？

为了解某校八年级学生一门课程的学习情况，小佳和小丽分别对八年级1班和2班本门课程的期末成绩进行了调查分析．

小佳对八年级1班全班学生 $(25$名）的成绩进行分析，过程如下：

收集、整理数据：

表一

分数段 班级	$60⩽x<70$	$70⩽x<80$	$80⩽x<90$	$90⩽x⩽100$
八年级1班	7	5	10	3

分析数据：

表二

统计量 班级	平均数	中位数	众数	极差	方差
八年级1班	78		85	36	105.28

小丽用同样的方法对八年级2班全班学生 $(25$名）的成绩进行分析，数据如下：

表三

统计量 班级	平均数	中位数	众数	极差	方差
八年级2班	75	76	73	44	146.80

根据以上信息，解决下列问题：

（1）已知八年级1班学生的成绩在 $80⩽x<90$这一组的数据如下：

85，87，88，80，82，85，83，85，87，85

根据上述数据，将表二补充完整；

（2）你认为哪个班级的成绩更为优异？请说明理由．

为了调查甲、乙两台包装机分装标准质量为奶粉的情况，质检员进行了抽样调查，过程如下，请补全表一、表二中的空白，并回答提出的问题．

收集数据：

从甲、乙包装机分装的奶粉中各自随机抽取10袋，测得实际质量（单位：如下：

甲：400，400，408，406，410，409，400，393，394，395

乙：403，404，396，399，402，402，405，397，402，398

整理数据：

表一

质量 频数 种类
甲	3	0	3	0	1	3
乙	0		1	5		0

分析数据：

表二

种类	平均数	中位数	众数	方差
甲	401.5		400	36.85
乙	400.8	402		8.56

得出结论：

包装机分装情况比较好的是　　（填甲或乙），说明你的理由．