初中数学统计量的选择解答题

某市努力改造空气质量，近年来空气质量明显好转，根据市环境保护局公布的2006—2010这五年各年的全年空气质量优良的天数，绘制折线图如图所示，根据图中的信息回答：

（1）这五年的全年空气质量优良天数的中位数是        ，极差是      ；
（2）这五年的全年空气质量优良天数与它前一年相比较，增加最多的是     年，（填写年份）
（3）求这五年的全年空气质量优良天数的平均数。

要从甲、乙两名同学中选出一名，代表班级参加射击比赛，如图是两人最近10次射击训练成绩的折线统计图．

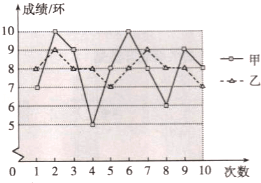
（1）已求得甲的平均成绩为8环，求乙的平均成绩；
（2）观察图形，直接写出甲，乙这10次射击成绩的方差s_甲²，   s_乙²哪个大；
（3）如果其他班级参赛选手的射击成绩都在7环左右，本班应该选      参赛更合适；如果其他班级参赛选手的射击成绩都在9环左右，本班应该选      参赛更合适．

下表是某校九年级（1）班20名学生某次数学测验的成绩统计表：

成绩	60	70	80	90	100
人数（人）	1	5	x	y	2

 
（1）若这20名学生的平均分是84分，求x和y的值；
（2）这20名学生的本次测验成绩的众数和中位数分别是多少？

雅安地震，牵动着全国人民的心，地震后某中学举行了爱心捐款活动，下图是该校九年级某班学生为雅安灾区捐款情况绘制的不完整的条形统计图和扇形统计图．

（1）求该班人数；（2）补全条形统计图；
（3）在扇形统计图中，捐款“15元人数”所在扇形的圆心角∠AOB的度数；
（4）若该校九年级有800人，据此样本，请你估计该校九年级学生共捐款多少元？

（本题10分）某学习小组想了解扬州市“迎建城2500周年”健身活动的开展情况，准备采用以下调查方式中的一种进行调查：①从一个社区随机选取200名居民；②从一个城镇的不同住宅楼中随机选取200名居民；③从该市公安局户籍管理处随机抽取200名城乡居民作为调查对象．
（1）在上述调查方式中，你认为最合理的是         (填序号)；
（2）由一种比较合理的调查方式所得到的数据制成了如图所示的频数分布直方图，请直接写出这200名居民健身时间的众数、中位数；
（3）小明在求这200名居民每人健身时间的平均数时，他是这样分析的：

小明的分析正确吗？如果不正确，请求出正确的平均数；
（4）若我市有800万人，估计我市每天锻炼2小时及以上的人数是多少？

某中学举行“校园好声音”歌手大赛，初、高中部根据初赛成绩，各选出5 名选手组成初中代表队和高中代表队参加学校决赛．每个队5 名选手的决赛成绩如图所示：

（1）填表：

（2）结合两队决赛成绩的平均数和中位数，分析哪个代表队的成绩较好；
（3）计算两队决赛成绩的方差，并判断哪个代表队的成绩较为稳定．

为了解学生零花钱的使用情况，校团委随机调查了本校部分学生每人一周的零花钱数额，并绘制了如图甲、乙所示的两个统计图（部分未完成）．请根据图中信息，回答下列问题：

（1）校团委随机调查了多少学生？请你补全条形统计图；
（2）表示“50元”的扇形的圆心角是多少度？补调查的学生每人一周零花钱数额的中位数是多少元？
（3）四川地震后，全校1000名学生每人自发地捐出一周零花钱的一半，以支援灾区建设．请估算全校学生共捐款多少元？

射击集训队在一个月的集训中，对甲、乙两名运动员进行了10次测试，成绩如图（折线图中，粗线表示甲，细线表示乙）：

（1）根据图中所提供的信息填写下表：

	平均数	众数	方差
甲	7
乙			2．2

 
（2）请从下列四个不同的角度对测试结果进行分析：
①从平均数和方差结合看_______的成绩好；
②从平均数和众数结合看_______的成绩好；
③从折线图上两人射击环数的走势看_____更有潜力．
④如果你是教练，会选择哪位运动员参加比赛？说明理由．

某班为了从甲、乙两同学中选出班长，进行了一次演讲答辩和民主测评，A、B、C、D、E五位老师作为评委，对“演讲答辩”情况进行了评价，全班50位同学参与了民主测评，结果如下表：

规则：①演讲答辩得分按“去掉一个最高分和一个最低分后，再算出平均分”的方法确定；②民主测评得分=“好”票数×2分+“较好”票数×1分+“一般”票数×0分；③演讲答辩得分和民主测评得分按4：6确定权重，计算综合得分，请你计算一下甲、乙的综合得分，选出班长．

某厂为了解工人在单位时间内加工同一种零件的技能水平，随机抽取了50名工人加工的零件进行检测，统计出他们各自加工的合格品数是1﹣8这8个整数，现提供统计图的部分信息如图，请解答下列问题：

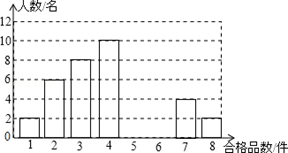
（1）根据统计图，求这50名工人加工出的合格品数的中位数；
（2）写出这50名工人加工出的合格品数的众数的可能取值；
（3）厂方认定，工人在单位时间内加工出的合格品数不低于3件为技能合格，否则，将接受技能再培训．已知该厂有同类工人400名，请估计该厂将接受技能再培训的人数．

九（2）班组织了一次经典朗读比赛，甲、乙两队各10人的比赛成绩如下表（10分制）：

甲	7	8	9	7	10	10	9	10	10	10
乙	10	8	7	9	8	10	10	9	10	9

 
（1）甲队成绩的中位数是     分，乙队成绩的众数是      分；
（2）计算乙队的平均成绩和方差；
（3）已知甲队成绩的方差是1．4，则成绩较为整齐的是     队

（.天津市，第20题，8分） （本小题8分）
某商场服装部为了解服装的销售情况，统计了每位营业员在某月的销售额（单位：万元），并根据统计的这组销售额数据，绘制出如下的统计图①和图②. 请根据相关信息，解答下列问题：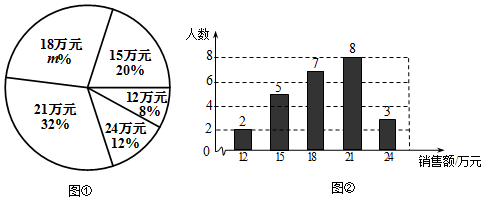

（Ⅰ）该商场服装部营业员人数为_________图①中m的值为_________；
（Ⅱ）求统计的这组销售额数据的平均数、众数和中位数.

（.河南省，第18题，9分）为了了解市民“获取新闻的最主要途径”，某市记者开展了一次抽样调查，根据调查结果绘制了如下尚不完整的统计图.

根据以上信息解答下列问题：
（1）这次接受调查的市民总人数是           ；
（2）扇形统计图中，“电视”所对应的圆心角的度数是           ；
（3）请补全条形统计图；
（4）若该市约有80万人，请你估计其中将“电脑和手机上网”作为“获取新闻的最主要途径”的总人数.

（.河北省，第24题，11分） （本小题满分11分）
某厂生产A，B两种产品.其单价随市场变化而做相应调整.营销人员根据前三次单价变化的情况，绘制了如下统计表及不完整的折线图：
A，B产品单价变化统计表

	第一次	第二次	第三次
A产品单价（元/件）	6	52	63.5
B产品单价（元/件）	3.5	4	3

并求得A产品三次单价的平均数和方差：
：.
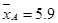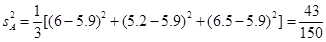（1）补全图中B产品单价变化的折线图.B产品第三次的单价比上一次的单价降低了____%；
（2）求B产品三次单价的方差，并比较哪种产品的单价波动小：
（3）该厂决定第四次调价，A产品的单价仍为6.5元/件，B产品的单价比3元/件上调m%（m＞0），使得A产品这四次单价的中位数是B产品四次单价中位数的2倍少1.求m的值.

某校为了开阔学生的视野，积极组织学生参加课外读书活动．“放飞梦想”读书小组协助老师随机抽取本校的部分学生，调查他们最喜爱的图书类别（图书分为文学类、艺体类、科普类、其他等四类），并将调查结果绘制成如下两幅不完整的统计图，请你结合图中的信息解答下列问题：
（1）求被调查的学生人数；
（2）补全条形统计图；
（3）已知该校有1200名学生，估计全校最喜爱文学类图书的学生有多少人？