初中数学利用频率估计概率试题

如图，A．B两个转盘分别被分成三个、四个相同的扇形，分别转动A盘、B盘各一次（若指针恰好指在分割线上，则重转一次，直到指针指向一个数字为止）．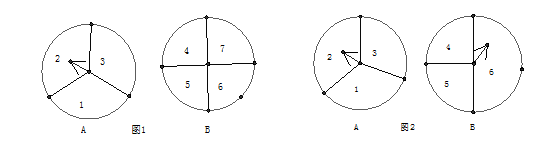

（1） 如图1，两个指针所指的区域内的数字之和大于7的概率为_________；
（2） 如果将图1中的转盘改为图2，其余不变，用列表或画树状图的方法，求两个指针所知区域的数字之和大于7 的概率．

一个不透明的口袋里有10个黑球和若干个黄球，从口袋中随机摸出一球记下其颜色，再把它放回口袋中摇匀，重复上述过程，共试验200次，其中有120次摸到黄球，由此估计袋中的黄球有______个．

下列事件中，①投掷一枚普通骰子，朝上一面的点数是3；②从2、4、6、8、10这5张卡片中任抽一张是奇数；③任意抛掷一枚硬币，正面朝上；④从装有一个红球三个黄球的袋子中任取两球，至少有一个是黄球．其中是必然事件的有               （填序号即可）．

一个不透明的布袋里装有7个只有颜色不同的球，其中4个红球，3个白球，从布袋中随机摸出一个球，摸出的球是红球的概率是（   ）

A．

B．

C．

D．

（本小题8分）一只不透明的袋子里共有4个球，其中3个白球，1个红球，它们除颜色外均相同．
（1）从袋子中随机摸出一个球是白球的概率是多少？
（2）从袋子中随机摸出一个球，不放回袋子，摇匀袋子后再摸一个球，请用列表或画树状图的方法，求出两次摸出的球都是白球的概率．

（本小题8分）甲、乙两位同学玩转盘游戏，游戏规则：将圆盘平均分成三份，分别涂上红，黄，绿三种颜色，两位同学分别转动转盘两次（若压线，重新转）．若两次指针指到的颜色相同，则甲获胜；若两次指针指到的颜色是黄绿组合则乙获胜；其余情况则视为平局．

（1）请用画树状图的方法，列出所有可能出现的结果；
（2）试用概率说明游戏是否公平．

如图所示是一飞镖游戏板，大圆的直径把一组同心圆分成四等份，假设飞镖击中圆面上每一个点都是等可能的，则飞镖落在黑色区域的概率是      ．

“上升数”是一个数中右边数字比左边数字大的自然数（如：34,568,2468），任取一个两位数，是“上升数”的概率是（   ）

A．

B．

C．

D．

下列事件中，是必然事件的是（ ）

A．抛掷一枚质地均匀的硬币，落地后正面朝上

B．海安县7月份某一天的最低气温是﹣3℃

C．通常加热到100℃时，水沸腾

D．打开电视，正在播放综艺节目《一站到底》

如图14是某市9月1日至10日的空气质量指数趋势图，空气质量指数小于100表示空气质量优良，空气质量指数大于200表示空气重度污染，某人随机选择9月1日至9月8日中的某一天到达该市，并连续停留3天，则此人在该市停留期间有且仅有1天空气质量优良的概率是           ．

在a²□4a□4空格□中，任意填上“+”或“—”，在所得到的所有代数式中，能构成完全平方式的概率是（  ）

A．1

B．

C．

D．

小张同学报名参加校运动会，有下列5个项目可供选择：
径赛项目：100m，200m，800m （分别用A1、A2、 A3表示）；
田赛项目：立定跳远，跳高（分别用B1、B2表示）
（1）小张从5个项目中任选一个，恰好是径赛项目的概率为         ；
（2）小张从5个项目中任选两个，利用树状图或表格列举出所有可能的结果，并求恰好是一个田赛项目和一个径赛项目的概率

事件A发生的概率为0．05，大量重复做这种试验，事件A平均每100次发生的次数是    ．

有一种竞猜游戏的规则如下：在20个商标牌中，有5个商标牌的背面注明一定的奖金额，其余商标牌的背面是一张哭脸，若翻到哭脸就不得奖．小王随机翻动一个商标牌，那么他获奖的概率是   （   ）

A．

B．

C．

D．

桌面上放有4张卡片，正面分别标有数字1，2，3，4．这些卡片除数字外完全相同，把这些卡片反面朝上洗匀后放在桌面上，甲从中任意抽出一张，记下卡片上的数字后仍反面朝上放回洗匀，乙也从中任意抽出一张，记下卡片上的数字，然后将这两数相加．
（1）请用列表或画树状图的方法求两数之和为5的概率；
（2）若甲与乙按上述方式做游戏，当两数之和为5时，甲胜；当两数之和不为5时，则乙胜．若甲胜一次得12分，谁先达到120分为胜．那么乙胜一次得多少分，这个游戏对双方公平？