初中数学利用频率估计概率选择题

某校体育节有13名同学参加女子百米赛跑，它们预赛的成绩各不相同，取前6名参加决赛．小颖已经知道了自己的成绩，她想知道自己能否进入决赛，还需要知道这13名同学成绩的（  ）

A．方差

B．极差

C．中位数

D．平均数

分别用写有“金华”、“文明”、“城市”的字块拼句子，那么能够排成“金华文明城市”或“文明城市金华”的概率是（    ）

A．

B．

C．

D．

某十字路口的交通信号灯每分钟红灯亮30秒，绿灯亮25秒，黄灯亮5秒，当你抬头看信号灯时，是黄灯的概率为（ ）

A．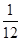

B．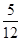

C．

D．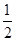

一个盒子里有完全相同的三个小球，球上分别标有数字﹣2，1，4．随机摸出一个小球（不放回），其数字为p，再随机摸出另一个小球其数字记为q，则满足关于x的方程x²+px+q=0有实数根的概率是（ ）

A．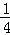

B．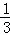

C．

D．

在一个不透明的盒子中，装有4个黑球和若干个白球，它们除颜色外没有任何其他区别．摇匀后从中随机摸出一个球记下颜色，再把它放回盒子中．不断重复以上操作过程，共摸了100次球，发现有20次摸到黑球，据此估计盒子中白球的个数为（   ）

A．12个

B．16个

C．20个

D．30个

随机掷一枚均匀的硬币两次，两次都是正面的概率是（  ）

A．

B．

C．

D．无法确定

在李咏主持的“幸运52”栏目中，曾有一种竞猜游戏，游戏规则是：在20个商标牌中，有5个商标牌的背面注明了一定的奖金，其余商标牌的背面是一张“哭脸”，若翻到“哭脸”就不获奖,参与这个游戏的观众有三次翻牌的机会，且翻过的牌不能再翻．有一位观众已翻牌两次，一次获奖，一次不获奖，那么这位观众第三次翻牌获奖的概率是（   ）

A．

B．

C．

D．

一个布袋里装有只有颜色不同的5个球，其中3个红球，2个白球。从中任意摸出1个球，记下颜色后放回，搅匀，再任意摸出1个球，摸出的2个球都是红球的概率是（   ）

A．

B．

C．

D．

有5张大小、背面都相同的扑克牌，正面上的数字分别是4，5，6，7，8．若将这5张牌背面朝上洗匀后，从中任意抽取1张，那么这张牌正面上的数字为偶数的概率是（ ）

A．

B．

C．

D．

下列事件中，必然事件是（   ）

A．打开电视机，正在播放体育比赛

B．明天是星期一

C．掷一枚均匀的硬币，正面朝上

D．在北半球，太阳会从东方升起

小明在白纸上任意画了一个锐角，他画的角在45º到60º之间的概率是（   ）

A．

B．

C．

D．

下列事件中，必然事件是(    )、

A．打开电视，它正在播广告	B．掷两枚质地均匀I
C．早晨的太阳从东方升起	D．没有水分，种子发芽

下列五幅图是世博会吉祥物照片，质地大小、背面图案都一样，把它们充分洗匀后翻放在桌面上，则抽到2010年上海世博会吉祥物照片的概率是(    )

A．

B．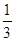

C．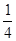

D．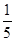

某射击运动员在同一条件下的射击成绩记录如下：

射击次数	20	80	100	200	400	1000
"射中九环以上"的次数	18	68	82	168	327	823
"射中九环以上"的频率（结果保留两位小数）	0.90	0.85	0.82	0.84	0.82	0.82

根据频率的稳定性，估计这名运动员射击一次时"射中九环以上"的概率约是 $($ 　　 $)$

A．

0.90

B．

0.82

C．

0.85

D．

0.84

甲、乙、丙3人聚会，每人带了一件从外盒包装上看完全相同的礼物（里面的东西只有颜色不同），将3件礼物放在一起，每人从中随机抽取一件．
（1）下列事件是必然事件的是（   ） 
A、乙抽到一件礼物
B、乙恰好抽到自己带来的礼物
C、乙没有抽到自己带来的礼物
D、只有乙抽到自己带来的礼物
（2）甲、乙、丙3人抽到的都不是自己带来的礼物（记为事件A），请列出事件A的所有可能的结果，并求事件A的概率．