(8分)在一个不透明的口袋里装有若干个相同的红球, 为了估计袋中红球的数量，某学习小组做了摸球实验, 他们将30个与红球大小形状完全相同的白球装入袋中，搅匀后从中随机摸出一个球并记下颜色, 再把它放回袋中, 不断重复. 下表是几次活动汇总后统计的数据：（1） 请估计：当次数
很大时, 摸到白球的频率将会接近 ；假如你去摸一次, 你摸到红球的概率是 ；（精确到0.1）.（2） 试估算口袋中红球有多少只?
（3）解决了上面的问题后请你从统计与概率方面谈一条启示.
| 摸球的次数 |
150 |
200 |
500 |
900 |
1000 |
1200 |
摸到白球的频数 |
51 |
64 |
156 |
275 |
303 |
361 |
摸到白球的频率 |
0.34 |
0.32 |
0.312 |
0.306 |
0.303 |
0.301 |
(本题满分10分)有3张不透明的卡片，除正面写有不同的数字外，其他均相同．将这三张卡片背面朝上洗匀后，第一次从中随机抽取一张，并把这张卡片上标有的数字记为一次函数关系式中的k，第二次从余下的两张卡片中再随机抽取一张，将上面标有的数字记为一次函数关系式中的b．
(1)写出k为负数的概率．
(2)求一次函数y＝kx＋b的图象经过第二、三、四象限的概率(用画树状图或列表的方法求解)．
某初级中学准备随机选出七、八、九三个年级各1名学生担任领操员．现已知这三个年级分别选送一男、一女共6名学生为备选人.（1）请你利用树状图或表格列出所有可能的选法；
（2）求选出“两男一女”三名领操员的概率．
有四张背面相同的纸牌A，B，C，D，其正面分别画有四个不同的几何图形（如图）．小明将这4张纸牌背面朝上洗匀后摸出一张，将剩余3张洗匀后再摸出一张．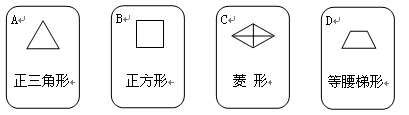
（1）用树状图（或列表法）表示两次摸牌所有可能出现的结果（纸牌用A，B，C，D表示）；
（2）求摸出的两张牌面图形既是轴对称图形又是中心对称图形纸牌的概率．
（本小题满分10分）
甲口袋中装有两个相同的小球，它们分别写有1和2；乙口袋中装有三个相同的小球，它们分别写有3、4和5；丙口袋中装有两个相同的小球，它们分别写有6和7．从这3个口袋中各随机地取出1个小球．（1）取出的3个小球上恰好有两个偶数的概率是多少？
（2）取出的3个小球上全是奇数的概率是多少？
(本题满分7分)甲，乙两个盒子中装有质地、大小相同的小球．甲盒中有2个白球、l个黄球和l个蓝球；乙盘中有l个白球、2个黄球和若干个蓝球．从乙盒中任意摸取一球为蓝球的概率是从甲盒中任意摸取一球
为蓝球的概率的2倍． (1) 求乙盒中蓝球的个数；
(2)从甲、乙两盒中分别任意摸取一球．求这两球均为蓝球的概率．
将背面相同，正面分别标有数字1、2、3、4的四张卡片洗匀后，背面朝上放在桌子上。⑴从中随机抽取两张卡片，求卡片正面上的数字之和大于4的概率；
⑵若先从中随机抽取一张卡片(不放回)，将该卡片正面上的数字作为十位上的数字；再随机抽取一张，将该卡片正面上的数字作为个位上的数字，求组成的两位数恰好是3的倍数的概率（请用树状图或列表法加以说明）．
某市今年的信息技术结业考试，采用学生抽签的方式决定自己的考试内容。规定：每位考生先在三个笔试题（题签分别用代码
表示）中抽取一个，再在三个上机题（题签分别用代码
表示）中抽取一个进行考试.小亮在看不到题签的情况下，分别从笔试题和上机题中随机地各抽取一个题签.（1）用树状图或列表法表示出所有可能的结构；
（2）求小亮抽到的笔试题和上机题的题签代码的下标（例如“
”的下表为“1”）均为奇数的概率.
（本小题满分6分）
2010年上海世博会某展览馆展览厅东面有两个入口A、B，南面、西面、北面各有一个出口，示意图如图所示．小华任选一个入口进入展览大厅，参观结束后任选一个出口离开．
（1）她从进入到离开共有多少种可能的结果（要求画出树状图）？
（2）她从入口A进入展厅并从北出口或西出口离开的概率是多少？
(本题满分12分)
节假日，小明和哥哥在水族馆看完海洋动物后，参加了出口处的抽奖活动．游戏的规则如下：每张门票只可摸球一次，每次从装有大小形状相同的2个白球和1个红球的盒子中，随机摸出一个球，若摸出的是红球，则获得一份奖品．(1) 求每次摸球中奖的概率？
(2) 小明想：我有二张票，中奖的概率就翻一倍．你认为小明的思考正确吗？请用列表法或画树形图分析说明．
在科技馆里，小亮看见一台名为帕斯卡三角的仪器，如图所示，当一实心小球从入口落下，它在依次碰到每层菱形挡块时，会等可能地向左或向右落下．
【命题1】试问小球通过第二层
位置的概率是多少？
【命题2】请用学过的数学方法模拟试验，并具体说明小球下落到第三层
位置第四层
位置处的概率各是多少？
小明想给小东打电话，但忘记了电话号码中的一位数字，只记得号码是284□9456（□表示忘记的数字）⑴若小明从0至9的自然数中随机选取一个数字放在□位置，求他正确拨打小东电话的概率；
⑵若□位置的数字是不等式组
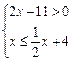的整数解，求□可能表示的数字．
小英和小丽用两个转盘做“配紫色”游戏，配成紫色小英得1分，否则小丽得1分，这个游戏对双方公平吗？（红色+蓝色=紫色，配成紫色者胜）
一个不透明的布袋里装有4个大小、质地均相同的乒乓球，每个球上面分别标有1、2、3、4，小林先从布袋中随机抽取一个乒乓球（不放回去），再从剩下的3个球中随机抽取第二个乒乓球。
请你列出所有可能的结果；
如图，有两个可以自由转动的均匀转盘A、B，转盘A被均匀地分成4等份，每份分别标上1、2、3、4四个数字；转盘B被均匀地分成6等份，每份分别标上1、2、3、4、5、6六个数字。有人为甲、乙两人设计了一个游戏，其规则如下：
⑴同时自由转动转盘A与B；
⑵转盘停止后，指针各指向一个数字（如果指针恰好指在分格线上，那么重转一次，直到指针停留在某一数字为止），用所指的两个数字作乘积，如果得到的积是偶数，那么甲胜；如果得到的积是奇数，那么乙胜（如转盘A指针指向3，转盘B指针指向5，3×5＝15，按规则乙胜）。你认为这样的规则是否公平？请说明理由；如果不公平，请你设计一个公平的规则，并说明理由。
试题篮
()
粤公网安备 44130202000953号
