初中数学利用频率估计概率试题

在一个黑色的布口袋里装着白、红、黑三种颜色的小球，它们除了颜色之外没有其它区别，其中白球2只、红球1只、黑球1只. 袋中的球已经搅匀．
（1）随机地从袋中摸出1只球，则摸出白球的概率是多少？
（2）随机地从袋中摸出1只球，放回搅匀再摸出第二个球.请你用画树状图或列表的方法表示所有等可能的结果，并求两次都摸出白球的概率．

有四张正面分别标有数字－2，－1，1，2的不透明卡片，它们除数字不同外其余相同。现将它们背面朝上，洗匀后小李从中任取两张，将该卡片上的数字这和记为x，则小李得到的x值使分式的值为0的概率是________.

小张的三位朋友甲、乙、丙想破译他在电脑中设置的登录密码．但是他们只知道这个密码共有五位数字．他们根据小张平时开电脑时输入密码的手势，分别猜测密码是“51932”、“85778”或“74906”．实际上他们每个人都只猜对了密码中对应位置不相邻的两个数字．由此你知道小张设置的密码是________．

以下四个命题：
①每一条对角线都平分一组对角的平行四边形是菱形．
②当m > 0时， y =–mx＋1与 两个函数都是y随着x的增大而减小．
③已知正方形的对称中心在坐标原点，顶点A，B，C，D按逆时针依次排列，若A点坐标为（1，）则D点坐标为（1，）.
④在一个不透明的袋子中装有标号为1，2，3，4的四个完全相同的小球，从袋中随机摸取一个然后放回，再从袋中随机地摸取一个，则两次取到的小球标号的和等于4的概率为．
其中正确的命题有       （只需填正确命题的序号）

在数-1，1，2中任取两个数作为点坐标，那么该点刚好在一次函数图象上的概率是（ ）

A．

B．

C．

D．

完全相同的4个小球，上面分别标有数字1、－1、2、－2，将其放入一个不透明的盒子中摇匀，再从中随机摸球两次．把第一次、第二次摸到的球上标有的数字分别记作m、n，以m、n分别作为一个点的横坐标与纵坐标，
（1）若第一次摸出球后放回摇匀，求点（m，n）不在第二象限的概率．（用列表法求解）
（2）若第一次摸出球后不放回，求点（m，n）不在第二象限的概率．（用树状图求解）

在一个不透明的口袋中有四个手感完全一致的小球，四个小球上分别标有数字－4，－1,  2,  5；
（1）从口袋中随机摸出一个小球，其上标明的数是奇数的概率是多少？
（2）从口袋中随机摸出一个小球不放回，再从中摸出第二个小球：
①请用表格或树状图表示先后摸出的两个小球所标数字组成的可能结果？
②求依次摸出的两个小球所标数字为横坐标，纵坐标的点位于第四象限的概率．

我区实施新课程改革后，学生的自主字习、合作交流能力有很大提高．张老师为了了解所教班级学生自主学习、合作交流的具体情况，对本班部分学生进行了为期半个月的跟踪调査，并将调査结果分成四类，A：特别好；B：好；C：一般；D：较差；并将调査结果绘制成以下两幅不完整的统计图，请你根据统计图解答下列问题：

（1）本次调查中，张老师一共调査了 名同学，其中C类女生有 名，D类男生有 名；
（2）将上面的条形统计图补充完整；
（3）为了共同进步，张老师想从被调査的A类和D类学生中分别选取一位同学进行“一帮一”互助学习，请用列表法或画树形图的方法求出所选两位同学恰好是一位男同学和一位女同学的概率．

学校组织春游，安排九年级三辆车，小明与小慧都可以从这三辆车中任意选一辆搭乘。
（1）用树状图（或列表法）表示小明与小慧乘车所有可能出现的结果`（三辆车分别用甲、乙、丙表示）；
（2）求小明与小慧乘车不同的概率有多大？

有A、B两个黑布袋，A布袋中有两个完全相同的小球，分别标有数字1和2，B布袋中有三个完全相同的小球，分别标有数字－1，－2和－3，小强从A布袋中随机取出一个小球，记录其标有的数字为a，再从B布袋中随机取出一个小球，记录其标有的数字为b，这样就确定一个点Q的坐标为（a，b）
（1）用列表或树状图的方法写出点Q的所有可能坐标
（2）求点Q落在直线y=x－3上的概率

王老师为了了解学生在数学学习中常见错误的纠正情况,收集整理了学生在作业和考试中的常见错误,编制了10道选择题,每题3分,对他所教的初三(1)班和(2)班进行了检测.如图表示从两班各随机抽取的10名学生的得分情况:
(1)利用图中提供的信息,补全下表:

班级	平均数(分)	中位数(分)	众数(分)
(1)班		24	24
(2)班	24

(2)若把24分以上(含24分)记为”优秀”,两班各40名学生,请估计两班各有多少名学生成绩优秀;
(3)观察图中数据分布情况,你认为哪个班的学生纠错的得分情况比较整齐一些,并
说明原因.

有正面分别标有数字、、、、的五张不透明卡片，它们除数字不同外其余全部相同，现将它们背面朝上，洗匀后从中任取一张，将卡片上的数字记为，则使关于的方程+x－m=0有实数解且关于的不等式组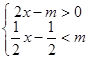有整数解的的概率为    ．

有红、黄、蓝、白4色小球各10个，混合放在一个暗盒中．一次至少摸出         个，才能保证有6个小球是同种颜色．

已知M（a，b）是平面直角坐标系xOy中的点，其中a是从l，2，3三个数中任取的一个数，b是从l，2，3，4四个数中任取的一个数．定义“点M（a，b）在直线x+y=n上”为事件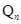 （2≤n≤7，n为整数），则当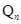的概率最大时，n的所有可能的值为           ．

四张大小、质地均相同的卡片上分别标有：1，2，3，4．现将标有数字的一面朝下扣在桌子上，然后由小明从中随机抽取一张（不放回），再从剩下的3张中随机取第二张．
（1）用画树状图的方法，列出小明前后两次取得的卡片上所标数字的所有可能情况；
（2）求取到的两张卡片上的数字之积为奇数的概率．