有3张扑克牌,分别是红桃3、红桃4和黑桃5.把牌洗匀后甲先抽取一张,记
下花色和数字后将牌放回,洗匀后乙再抽取一张.
⑴先后两次抽得的数字分别记为s和t,则︱s-t︱≥1的概率.
⑵甲、乙两人做游戏,现有两种方案.A方案:若两次抽得相同花色则甲胜,否则乙胜.B方案:若两次抽得数字和为奇数则甲胜,否则乙胜.
请问甲选择哪种方案胜率更高?
中国象棋红方棋子按兵种不同分布如下:1个帅,5个兵,“士象、马、车、炮”各两个,将所有棋子反面朝上放在棋盘中,任取一个不是士、象、帅的概率是
一个口袋中有4个完全相同的小球,把它们分别标号为1,2,3,4.
(1)随机摸取一个小球,求恰好摸到标号为2的小球的概率;
(2)随机摸取一个小球然后放回,再随机摸取一个小球,求两次摸取的小球的标号的和为5的概率.
在4张卡片上分别写有1~4的整数,随机抽取一张后放回,再随机地抽取一张,那么第二次取出的数字能够整除第一次取出的数字的概率是.
为了加强食品安全管理,有关部门对某大型超市的甲、乙两种品牌食用油共抽
18瓶进行检测,检测结果分成“优秀”、“合格”、“不合格”三个等级,数据处理后制成以
下折线统计图和扇形统计图.
⑴甲、乙两种品牌食用油各被抽取了多少瓶用于检测?
⑵在该超市购买一瓶乙品牌食用油,请估计能买到“优秀”等级的概率是多少?
(11·贺州)在4张完全相同的卡片上分别画上图①、②、③、④.在看不见图
形的情况下随机抽取一张,卡片上的图形是中心对称图形的概率是 _ ▲ .
(11·贺州)在一个不透明的袋子中装有4个除颜色外完全相同的小球,其中黄球
1个,红球1个,白球2个,“从中任意摸出2个球,它们的颜色相同”这一事件
| A.必然事件 | B.不可能事件 | C.随机事件 | D.确定事件 |
(11·佛山)现在初中课本里所学习的概率计算问题只有以下类型:
第一类是可以列举有限个等可能发生的结果的概率计算问题(一步试验直接列举,两步以上的试验可以借助树状图或表格列举),比如掷一枚均匀硬币的试验;
第二类是用试验或者模拟试验的数据计算频率,并用频率估计概率的概率计算问题,比如掷图钉的试验;
解决概率计算问题,可以直接利用模型,也可以转化后再利用模型;
请解决以下问题
(1)如图,类似课本的一个寻宝游戏,若宝物随机藏在某一块砖下(图中每一块砖除颜色外完全相同),则宝物藏在阴影砖下的概率是多少 ?
?
(2)在 中随机选取3个整数,若以这3个整数为边长构成三角形的情况如下表:
中随机选取3个整数,若以这3个整数为边长构成三角形的情况如下表:
请你根据表中数据,估计构成钝角三角形的概率是多少?(精确到百分位)
经过某十字路口的汽车,它可能继续直行,也可能向左或向右转.若这三种可能性大小相同,则两辆汽车经过该十字路口全部继续直行的概率为( )
A.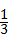 |
B.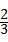 |
C.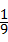 |
D.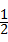 |
有三张正面分别写有数字﹣2,﹣1,1的卡片,它们的背面完全相同,将这三张卡片北背面朝上洗匀后随机抽取一张,以其正面的数字作为x的值,放回卡片洗匀,再从三张卡片中随机抽取一张,以其正面的数字作为y的值,两次结果记为(x,y).
(1)用树状图或列表法表示(x,y)所有可能出现的结果;
(2)求使分式 有意义的(x,y)出现的概率
有意义的(x,y)出现的概率
有正面分别标有数字 、
、 、
、 、
、 、
、 的五张不透明卡片,它们除数字不同外其余全部相同,现将它们背面朝上,洗匀后从中任取一张,将卡片上的数字记为
的五张不透明卡片,它们除数字不同外其余全部相同,现将它们背面朝上,洗匀后从中任取一张,将卡片上的数字记为 ,则使关于
,则使关于 的方程
的方程 +x-m=0有实数解且关于
+x-m=0有实数解且关于 的不等式组
的不等式组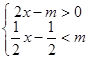 有整数解的的概率为 .
有整数解的的概率为 .
已知M(a,b)是平面直角坐标系xOy中的点,其中a是从l,2,3三个数中任取的一个数,b是从l,2,3,4四个数中任取的一个数.定义“点M(a,b)在直线x+y=n上”为事件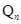 (2≤n≤7,n为整数),则当
(2≤n≤7,n为整数),则当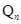 的概率最大时,n的所有可能的值为 .
的概率最大时,n的所有可能的值为 .
四张大小、质地均相同的卡片上分别标有:1,2,3,4.现将标有数字的一面朝下扣在桌子上,然后由小明从中随机抽取一张(不放回),再从剩下的3张中随机取第二张.
(1)用画树状图的方法,列出小明前后两次取得的卡片上所标数字的所有可能情况;
(2)求取到的两张卡片上的数字之积为奇数的概率.
试题篮
()