初中数学对称式和轮换对称式选择题

如图，边长为1的正方形ABCD绕点A逆时针旋转45°后得到正方形AB₁C₁D₁，边B₁C₁与CD交于点O，则四边形AB₁OD的面积是（　　）

A．

B．

C．

D．

如图，点B在x轴上，∠ABO=90°，∠A=30°，OA=4，将△OAB饶点O按顺时针方向旋转120°得到△OA′B′，则点A′的坐标是（　　）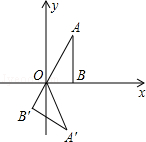

A．（2，﹣2）

B．（2，﹣2）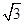

C．（2，﹣2）

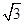D．（2，﹣2）

如图，四边形ABCD中，∠BAD＝110°，∠B＝∠D＝90°，在BC、CD上分别找一点M、N，使△AMN周长最小时，则∠AMN＋∠ANM的度数为

A．110° B．120° C．130° D．140°

如图，A（，1），B（1，），将∆AOB绕点O旋转150⁰后，得到∆A^’OB^’，则此时点A的对应点A^’的坐标为（）

A．（-，1）	B．（-2，0）
C．（-1，-）或（-2,0）	D．（-，-1）或（-2,0）

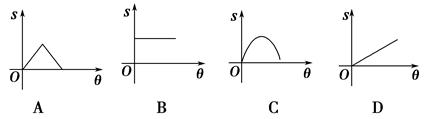
如图，两个边长相等的正方形ABCD和EFGH，正方形EFGH的顶点E固定在正方形ABCD的对称中心位置，正方形EFGH绕点E顺时针方向旋转，设它们重叠部分的面积为S，旋转的角度为θ，S与θ的函数关系的大致图象是（　　）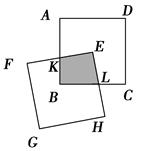

如图，正方形ABCD中，AB=6，点E在边CD上，且CD=3DE．将△ADE沿AE对折至△AFE，延长EF交边BC于点G，连接AG、CF．下列结论：①△ABG≌△AFG；②BG=GC；③AG∥CF；④S_△FGC=3．其中正确结论的个数是（　　）

A．1

B．2

C．3

D．4

如图，正方形ABCD的边长是3cm，一个边长为1cm的小正方形沿着正方形ABCD的边AB→BC→CD→DA→AB连续地翻转，那么这个小正方形第一次回到起始位置时，它的方向是( )


A. B. C. D.

在下列对称图形中，对称轴的条数最少的图形是（）

A．

B．等边三角形

C．正方形

D．正六边形

下列图形中，是轴对称而不是中心对称图形的是（　　）

A．平行四边形

B．菱形

C．等腰梯形

D．直角梯形

以下多边形中，既是轴对称图形又是中心对称图形的是【】

A．正五边形

B．矩形

C．等边三角形

D．平行四边形

点（－2，3）关于原点对称的点的坐标是

A．(2,3)

B．(－2,－3)

C．(2,－3)

D．(－3,2)

（11·贺州）如图，在方格纸中的△ABC经过变换得到△DEF，正确的变换是

A．把△ABC向右平移6格，

B．把△ABC向右平移4格，再向上平移1格

C．把△ABC绕着点A顺时针方向90º旋转，再右平移6格

D．把△ABC绕着点A顺时针方向90º旋转，再右平移6格

（11·佛山）一个图形无论经过平移还是旋转，有以下说法（）
①对应线段平行；②对应线段相等；
③对应角相等；④图形的形状和大小都没有发生变化

A．①②③

B．①②④

C．①③4

D．②③④

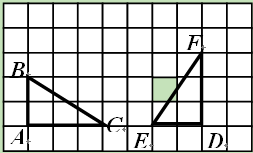
如图，点A、B、C、D、O都在方格纸的格点上，若△COD是由△AOB绕点O按逆时针方向旋转而得，则旋转的角度为（　　）

A、30° B、45°
C、90° D、135°

在下列图形中，既是轴对称图形，又是中心对称图形的是（　　）