初中数学对称式和轮换对称式计算题

如图1，已知∠DAC=90°，△ABC是等边三角形，点P为射线AD上任意一点（点P与点A不重合），连结CP，将线段CP绕点C顺时针旋转60°得到线段CQ，连结QB并延长交直线AD于点E．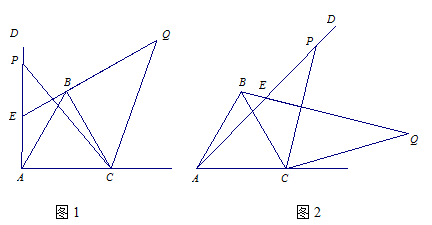

（1）如图1，猜想∠QEP=°；
（2）如图2，3，若当∠DAC是锐角或钝角时，其它条件不变，猜想∠QEP的度数，选取一种情况加以证明；
（3）如图3，若∠DAC=135°，∠ACP=15°，且AC=4，求BQ的长．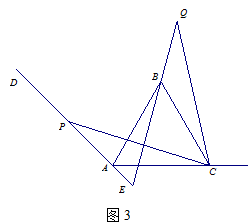

（本题6分）近年来，国家实施“村村通”工程和农村医疗卫生改革，某县计划在张村、李村之间建一座定点医疗站P，张、李两村座落在两相交公路内（如图所示）．医疗站必须满足下列条件：①使其到两公路距离相等；②到张、李两村的距离也相等．请用尺规作图确定P点的位置（保留作图痕迹，不必说明理由）．

已知：如图，△ABO是等边三角形，CD∥AB，分别交AO、BO的延长线于点C、D．求证：△OCD是等边三角形．

如图所示，折叠长方形一边AD，点D落在BC边的点F处，已知BC=10厘米，AB=8厘米，求EC的长。

已知：如图，直线l是线段AB的垂直平分线，C、D是l上任意两点（除AB的中点外）．求证：∠CAD=∠CBD．

如图，在△ABC中，点D是边BC的中点，DE⊥AB，DF⊥AC，垂足分别为点E、F，且DE=DF．试判断△ABC的形状，并证明你的结论．

已知等腰三角形的底角是顶角的2倍，求这个三角形各个内角的度数．

如图，有分别过A、B两个加油站的公路、相交于点O，现准备在∠AOB内建一个油库，要求油库的位置点P满足到A、B两个加油站的距离相等，而且P到两条公路、的距离也相等．请用尺规作图作出点P（不写作法，保留作图痕迹）

如图，在长度为1个单位长度的小正方形组成的正方形网格中，点A、B、C在小正方形的顶点上．

（1）在图中画出与△ABC关于直线成轴对称的△A；
（2） 线段被直线 ；
（3） 在直线上找一点P，使PB+PC的长最短，并算出这个最短长度．

已知：如图，BD为平行四边形ABCD的对角线，O为BD的中点，EF⊥BD于点O，与AD、BC分别交于点E、F．求证：DE=DF．

（本题6分） 如图，△ABC中，AB=AC，D是BC的中点，试说明AD⊥BC．

（本小题9分）如图，P是正方形ABCD内一点，连接PA、PB、PC，将△ABP绕点B顺时针旋转到△CBP′的位置．

（1）旋转中心是点 ______，点P旋转的度数是______；
（2）连接PP′，△BPP′的形状是 ______三角形；
（3）若PA=2，PB=4，∠APB=135°．
①求△BPP′的周长；②求PC的长．

实践与操作：如图1是以正方形两顶点为圆心，边长为半径，画两段相等的圆弧而成的轴对称图形，图2是以图1为基本图案经过图形变换拼成的一个中心对称图形．

（1）请你仿照图1，用两段相等圆弧（小于或等于半圆），在图3中重新设计一个不同的轴对称图形．
（2）以你在图3中所画的图形为基本图案，经过图形变换在图4中拼成一个中心对称图形．

已知：如图，锐角△ABC的两条高BD，CE相交于点O，且OB=OC．

（1）求证：△ABC是等腰三角形；
（2）判断点O是否在的平分线上，并说明理由．

如图，已知Rt△ABC中，∠ABC=90°，先把△ABC绕点B顺时针旋转90°至△DBE后，再把△ABC沿射线平移至△FEG，DE、FG相交于点H．

（1）判断线段DE、FG的位置关系，并说明理由；
（2）连结CG，求证：四边形CBEG是正方形．