初中数学对称式和轮换对称式解答题

如图1，已知∠DAC=90°，△ABC是等边三角形，点P为射线AD上任意一点（点P与点A不重合），连结CP，将线段CP绕点C顺时针旋转60°得到线段CQ，连结QB并延长交直线AD于点E．
（1）如图1，猜想∠QEP=      °；
（2）如图2，3，若当∠DAC是锐角或钝角时，其它条件不变，猜想∠QEP的度数，选取一种情况加以证明；
（3）如图3，若∠DAC=135°，∠ACP=15°，且AC=4，求BQ的长．

阅读下面材料：
小炎遇到这样一个问题：如图1，点E、F分别在正方形ABCD的边BC，CD上，∠EAF=45°，连结EF，则EF=BE+DF，试说明理由．
小炎是这样思考的：要想解决这个问题，首先应想办法将这些分散的线段相对集中．她先后尝试了翻折、旋转、平移的方法，最后发现线段AB，AD是共点并且相等的，于是找到解决问题的方法．她的方法是将△ABE绕着点A逆时针旋转90°得到△ADG，再利用全等的知识解决了这个问题（如图2）．
参考小炎同学思考问题的方法，解决下列问题：
（1）如图3，四边形ABCD中，AB=AD，∠BAD=90°点E，F分别在边BC，CD上，∠EAF=45°．若∠B，∠D都不是直角，则当∠B与∠D满足_       关系时，仍有EF=BE+DF；
（2）如图4，在△ABC中，∠BAC=90°，AB=AC，点D、E均在边BC上，且∠DAE=45°，若BD=1， EC=2，求DE的长．

在△ABC中，CA＝CB，在△AED中， DA＝DE，点D、E分别在CA、AB上．
（1）如图①，若∠ACB＝∠ADE＝90°，则CD与BE的数量关系是    ；
（2）若∠ACB＝∠ADE＝120°，将△AED绕点A旋转至如图②所示的位置，则CD与BE的数量关系是    ；，
（3）若∠ACB＝∠ADE＝2α（0°< α < 90°），将△AED绕点A旋转至如图③所示的位置，探究线段CD与BE的数量关系，并加以证明(用含α的式子表示)．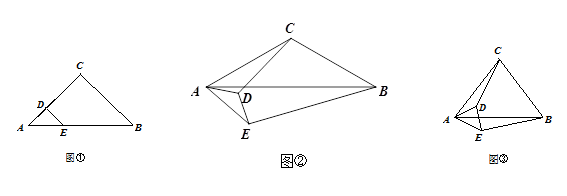

以下是小辰同学阅读的一份材料和思考：
五个边长为1的小正方形如图①放置，用两条线段把它们分割成三部分(如图②)，移动其中的两部分，与未移动的部分恰好拼接成一个无空隙无重叠的新正方形(如图③)．
小辰阅读后发现，拼接前后图形的面积相等，若设新的正方形的边长为x（x＞0），可得x²=5，x=.由此可知新正方形边长等于两个小正方形组成的矩形的对角线长．
参考上面的材料和小辰的思考方法，解决问题：
五个边长为1的小正方形（如图④放置），用两条线段把它们分割成四部分，移动其中的两部分，与未移动的部分恰好拼接成一个无空隙无重叠的矩形，且所得矩形的邻边之比为1：2．
具体要求如下：
（1）设拼接后的长方形的长为a，宽为b，则a的长度为          ；
（2）在图④中，画出符合题意的两条分割线（只要画出一种即可）；
（3）在图⑤中，画出拼接后符合题意的长方形（只要画出一种即可）

如图1，把边长分别是为4和2的两个正方形纸片OABC和OD′E′F′叠放在一起．
（1）操作1：固定正方形OABC，将正方形OD′E′F′绕点O按顺时针方向旋转45°得到正方形ODEF，如图2，连接AD、CF，线段AD与CF之间有怎样的数量关系？试证明你的结论；
（2）操作2，如图2，将正方形ODEF沿着射线DB以每秒1个单位的速度平移，平移后的正方形ODEF设为正方形PQMN，如图3，设正方形PQMN移动的时间为x秒，正方形PQMN与正方形OABC的重叠部分面积为y，直接写出y与x之间的函数解析式；
（3）操作3：固定正方形OABC，将正方形OD′E′F′绕点O按顺时针方向旋转90°得到正方形OHKL，如图4，求△ACK的面积．

把一张矩形ABCD纸片按如图方式折叠，使点A与点E重合，点C与点F重合（E、F两点均在BD上），折痕分别为BH、DG．
（1）求证：△BHE≌△DGF；
（2）若AB=6cm，BC=8cm，求线段FG的长．

(1)如图1，在△ABC中，BA＝BC，D，E是AC边上的两点，且满足∠DBE＝∠ABC(0°＜∠CBE＜∠ABC)，以点B为旋转中心，将△BEC按逆时针旋转，得到△BE′A(点C与点A重合，点E到点E′处)连接DE′.

求证：DE′＝DE.
(2)如图2，在△ABC中，BA＝BC，∠ABC＝90°，D，E是AC边上的两点，且满足∠DBE＝∠ABC(0°＜∠CBE＜∠45°)．

求证：DE²＝AD²＋EC².

如图，已知P是正方形ABCD内一点，PA=1，PB=2，PC=3，以点B为旋转中心，将△ABP沿顺时针方向旋转，使点A与点C重合，这时P点旋转到G点，连接BG、CG、PG。

（1）△ABP以点B为旋转中心旋转了            度；
（2）求出PG的长度；(3)以点G为圆心，r为半径作⊙G：
①当半径r满足                           时，⊙G与边PC只有一个交点;
②当半径r满足                           时，⊙G与边PC有两个交点;
③当半径r满足       时，⊙G与边PC没有交点。

解决下面问题：
如图，在△ABC中，∠A是锐角，点D，E分别在AB，AC上，且，BE与CD相交于点O，探究BD与CE之间的数量关系，并证明你的结论．

小新同学是这样思考的：
在平时的学习中，有这样的经验：假如△ABC是等腰三角形，那么在给定一组对应条件，如图a，BE，CD分别是两底角的平分线（或者如图b，BE，CD分别是两条腰的高线，或者如图c，BE，CD分别是两条腰的中线）时，依据图形的轴对称性，利用全等三角形和等腰三角形的有关知识就可证得更多相等的线段或相等的角.这个问题也许可以通过添加辅助线构造轴对称图形来解决．

图a                      图b                      图c
请参考小新同学的思路，解决上面这个问题．.

已知：四边形ABCD中,AD∥BC,AD=AB=CD,∠BAD=120°,点E是射线CD上的一个动点（与C、D不重合）,将△ADE绕点A顺时针旋转120°后,得到△ABE',连接EE'.
（1）如图1,∠AEE'=       °;

（2）如图2,如果将直线AE绕点A顺时针旋转30°后交直线BC于点F,过点E作EM∥AD交直线AF于点M,写出线段DE、BF、ME之间的数量关系;

（3）如图3,在（2）的条件下,如果CE=2,AE=,求ME的长.

翻转类的计算问题在全国各地的中考试卷中出现的频率很大，因此初三（5）班聪慧的小菲同学结合2011年苏州市数学中考卷的倒数第二题对这类问题进行了专门的研究。你能和小菲一起解决下列各问题吗？（以下各问只要求写出必要的计算过程和简洁的文字说明即可。）
（1）如图①，小菲同学把一个边长为1的正三角形纸片（即△OAB）放在直线l₁上，OA边与直线l₁重合，然后将三角形纸片向右翻转一周回到初始位置，求顶点O所经过的路程；并求顶点O所经过的路线；

图①
（2）小菲进行类比研究：如图②，她把边长为1的正方形纸片OABC放在直线l₂上，OA边与直线l₂重合，然后将正方形纸片向右翻转若干次．她提出了如下问题：

图②
问题①：若正方形纸片OABC接上述方法翻转一周回到初始位置，求顶点O经过的路程；
问题②：正方形纸片OABC按上述方法经过多少次旋转，顶点O经过的路程是。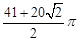
（3）①小菲又进行了进一步的拓展研究，若把这个正三角形的一边OA与这个正方形的一边OA重合（如图3），然后让这个正三角形在正方形上翻转，直到正三角形第一次回到初始位置（即OAB的相对位置和初始时一样），求顶点O所经过的总路程。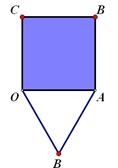

图③
②若把边长为1的正方形OABC放在边长为1的正五边形OABCD上翻转（如图④），直到正方形第一次回到初始位置，求顶点O所经过的总路程。

图④
（4）规律总结，边长相等的两个正多边形，其中一个在另一个上翻转，当翻转后第一次回到初始位置时，该正多边形翻转的次数一定是两正多边形边数的___________。

如图，矩形OABC在平面直角坐标系中，O为坐标原点，点A（0，4），C（2，0），将矩形OABC绕点O按顺时针方向旋转180⁰，得到矩形OEFG，顺次连接AC、CE、EG、GA.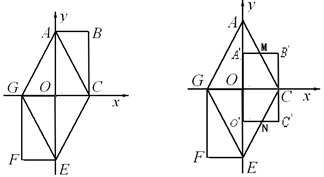

（1）请直接写出点F的坐标；
（2）试判断四边形ACEG的形状，并说明理由；
（3）将矩形OABC沿y轴向下平移m个单位（0＜m＜4），设平移过程中矩形与重叠部分面积为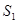，当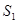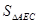：=11：16时，求m的值．

如图,在平面直角坐标系中,矩形OABC的两边OA、OC分别在x轴、y轴的正半轴上,OA=4,OC=2．点P从点O出发,沿x轴以每秒1个单位长的速度向点A匀速运动,当点P到达点A时停止运动,设点P运动的时间是t秒．将线段CP的中点绕点P按顺时针方向旋转90°得点D,点D随点P的运动而运动,连接DP、DA．

（1）请用含t的代数式表示出点D的坐标；
（2）求t为何值时,△DPA的面积最大,最大为多少？
（3）在点P从O向A运动的过程中,△DPA能否成为直角三角形？若能,求t的值．
若不能,请说明理由；
（4）请直接写出随着点P的运动,点D运动路线的长．

已知△ABC和△ADE是等腰直角三角形，∠ACB=∠ADE=90°，点F为BE中点，连结DF、CF.
（1）如图1,当点D在AB上，点E在AC上，请直接写出此时线段DF、CF的数量关系和位置关系（不用证明）；
（2）如图2，在（1）的条件下将△ADE绕点A顺时针旋转45°时，请你判断此时（1）中的结论是否仍然成立，并证明你的判断；
（3）如图3，在（1）的条件下将△ADE绕点A顺时针旋转90°时，若AD=1，AC=，求此时线段CF的长(直接写出结果).

阅读下列材料：
小华遇到这样一个问题,如图1,△ABC中,∠ACB=30º,BC=6,AC=5,在△ABC内部有一点P,连接PA.PB.PC,求PA+PB+PC的最小值．

小华是这样思考的：要解决这个问题,首先应想办法将这三条端点重合于一点的线段分离,然后再将它们连接成一条折线,并让折线的两个端点为定点,这样依据“两点之间,线段最短”,就可以求出这三条线段和的最小值了．他先后尝试了翻折.旋转.平移的方法,发现通过旋转可以解决这个问题．他的做法是,如图2,将△APC绕点C顺时针旋转60º,得到△EDC,连接PD.BE,则BE的长即为所求．
（1）请你写出图2中,PA+PB+PC的最小值为       ;
（2）参考小华的思考问题的方法,解决下列问题：
①如图3,菱形ABCD中,∠ABC=60º,在菱形ABCD内部有一点P,请在图3中画出并指明长度等于PA+PB+PC最小值的线段（保留画图痕迹,画出一条即可）;
②若①中菱形ABCD的边长为4,请直接写出当PA+PB+PC值最小时PB的长．