初中数学对称式和轮换对称式填空题

如图，在平面直角坐标系xOy中，已知抛物线y=﹣x（x﹣3）（0≤x≤3）在x轴上方的部分，记作C ₁，它与x轴交于点O，A ₁，将C ₁绕点A ₁旋转180°得C ₂，C ₂与x轴交于另一点A ₂．请继续操作并探究：将C ₂绕点A ₂旋转180°得C ₃，与x轴交于另一点A ₃；将C ₃绕点A ₂旋转180°得C ₄，与x轴交于另一点A ₄，这样依次得到x轴上的点A ₁，A ₂，A ₃，…，A _n，…，及抛物线C ₁，C ₂，…，C _n，…则C _n的顶点坐标为 （n为正整数，用含n的代数式表示）．

如图，等边△ABC在直角坐标系xOy中，已知，，点C绕点A顺时针方向旋转120°得到点C₁，点C₁绕点B顺时针方向旋转120°得到C₂，点C₂绕点C顺时针方向旋转150°得到点C₃，则点C₃的坐标是

如图，平面直角坐标系中，分别以点A（2，3）、点B（3，4）为圆心，1、3为半径作⊙A、⊙B，M，N分别是⊙A、⊙B上的动点，P为x轴上的动点，则PM+PN的最小值为

把边长为1的正方形纸片OABC放在直线m上，OA边在直线m上，然后将正方形纸片绕着顶点A按顺时针方向旋转90°，此时，点O运动到了点O₁处（即点B处），点C运动到了点C₁处，点B运动到了点B₁处，又将正方形纸片AO₁C₁B₁绕B₁点，按顺时针方向旋转90°…，按上述方法经过4次旋转后，顶点O经过的总路程为　　，经过61次旋转后，顶点O经过的总路程为　　．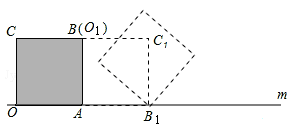

如图，在矩形ABCD中，AB=4，AD=10．连接BD，∠DBC的角平分线BE交DC于点E，现把△BCE绕点B逆时针旋转，记旋转后的△BCE为△BC′E′．当射线BE′和射线BC′都与线段AD相交时，设交点分别为F，G．若△BFD为等腰三角形，则线段DG长为 ．

把一张矩形纸片（矩形ABCD）按如图方式折叠，使顶点B和点D重合，折痕为EF．若AB = 3 cm，BC = 5 cm，则重叠部分△DEF的面积是cm²．

如图，在△BDE中，∠BDE="90" °，BD=2，点D的坐标是（3，0），∠BDO="15" °，将△BDE旋转到△ABC的位置，点C在BD上，则旋转中心的坐标为．

如图所示，两个全等的正方形ABCD与CDEF，旋转正方形ABCD能和正方形CDEF重合，则可以作为旋转中心的点有_________个。

）在直角坐标系中，一直线a向下平移3个单位后所得直线b经过点A（0，3），将直线b绕点A顺时针旋转60°后所得直线经过点B（-，0），则直线a的函数关系式为 ．

如图，平面直角坐标系中，A（-3，0），B（0，4），对△AOB按图示的方式连续作旋转变换，这样得到的第2014个三角形中，A点的对应点的坐标为.

如图，一段抛物线：y＝－x（x－3）（0≤x≤3），记为C1，它与x轴交于点O，A1；
将C1绕点A1旋转180°得C2，交x 轴于点A2；
将C2绕点A2旋转180°得C3，交x 轴于点A3；
……
如此进行下去，直至得C2015．若P（m，2）在第2015段抛物线C2015上，则m =_________．

如图，在Rt△ABC中，∠ACB=90°，AC=6，BC=8，AD是∠BAC的平分线．若P，Q分别是AD和AC上的动点，则PC+PQ的最小值是 ．

一段抛物线，记为，它与x轴交于点O，，将绕点旋转
180°得，交x 轴于点；将绕点旋转180°得C3，交x 轴于点；……如此进行下去，直至
得．若P（2015，m）在第672段抛物线上，则m = ．

如图，直线与x轴交于点B，与y轴交于点A，以线段AB为边，在第一象限内作正方形ABCD，点C落在双曲线（）上，将正方形ABCD沿x轴负方向平移a个单位长度，使点D恰好落在双曲线（）上的点D₁处，则a=．

如图，在⊿ABC中，∠A﹤90°，∠C=30°，AB=4，BC=6，E为AB的中点，P为AC边上一动点，将⊿ABC绕点B逆时针旋转角（）得到，点P的对应点为，连，在旋转过程中，线段的长度的最小值是．