初中数学对称式和轮换对称式填空题

如图，在⊿ABC中，∠A﹤90°，∠C=30°，AB=4，BC=6，E为AB的中点，P为AC边上一动点，将⊿ABC绕点B逆时针旋转角（）得到，点P的对应点为，连，在旋转过程中，线段的长度的最小值是        ．

如图，在直角坐标系中，四边形ABCD是正方形，A（1，-1）、B（-1，-1）、C（-1，1）、D（1， 1）.曲线AAAA…叫做“正方形的渐开线”，其中、、…的圆心依次是点B、C、D、A循环，则点A的坐标是          .

如图，圆柱形玻璃杯高为12cm、底面周长为18cm，在杯内离杯底4cm的点C处有一滴蜂蜜，此时一只蚂蚁正好在杯外壁，离杯上沿4cm与蜂蜜相对的点A处，则蚂蚁到达蜂蜜的最短距离为    cm．

如图，在等腰Rt△ABC中，∠A=90°，AC=9，点O在AC上，且AO=2，点P是AB上一动点，连接OP，将线段OP绕点O逆时针旋转90°得到线段OD，要使点D恰好落在BC边上，则OP的长等于                    ．

如图，第（1）个多边形由正三角形"扩展"而来，边数记，第（2）个多边形由正方形"扩展"而来，边数记为，…，依此类推，由正n边形"扩展"而来的多边形的边数记为（n≥3）.则的值是       ．

如图，从镜子中看到一钟表的时针和分针，此时的实际时刻是       ．

如图，Rt△ABC中，∠ACB＝90^o，AC＝12，BC＝5，D是AB边上的动点，E 是AC边上的动点，则BE＋ED的最小值为        ．

如图，在等腰直角三角形ABC中，∠ABC=90°E是AB上一点，BE=2，AE=3BE，P是AC上一动点．则PB+PE的最小值是      ．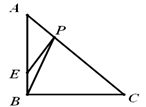

如图，等腰Rt△ABC中，∠ACB=90°，AC=BC=1，且AC边在直线a上，将△ABC绕点A顺时针旋转到位置①可得到点P₁，此时AP₁=；将位置①的三角形绕点P₁顺时针旋转到位置②，可得到点P₂，此时AP₂=1+；将位置②的三角形绕点P₂顺时针旋转到位置③，可得到点P₃，此时AP₃=2+；…，按此规律继续旋转，直至得到点P₂₀₁₄为止．则AP₂₀₁₄=　          ．

如图，在平面直角坐标系中，已知点P₀坐标为（1，0），将线段OP0绕点O顺时针方向旋转45°，再将其长度伸长为OP₀的2倍，得到线段OP₁；将线段OP₁绕点O顺时针方向旋转45°，再将其长度伸长为OP₁的2倍，得到线段OP₂，…，这样依次得到线段OP₃，OP₄，…，OP_n．则点P₂的坐标为             ；
当n=4m+1（m为自然数）时，点P_n的坐标为             ．

如图（1），有两个全等的正三角形ABC和ODE，点O、C分别为△ABC、△DEO的重心；固定点O，将△ODE顺时针旋转，使得OD经过点C，如图（2）所示，则图（2）中四边形OGCF与△OCH面积的比为           .

如图平行四边形ABCD中AB=AD=6，∠DAB=60度，F为AC上一点，E为AB中点，则EF+BF的最小值为        ．

如图，在正方形ABCD内作一个等边三角形ABE，连接DE、CE，有如下结论：①图中除等边三角形ABE外，还有三个等腰三角形；②△ADE≌△BCE；③此图形既是中心对称图形也是轴对称图形；④△ABE的面积与正方形ABCD的面积比是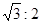；⑤△DEC与△ABE的面积比为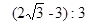。则以上结论正确的是          ．（只填正确结论的序号）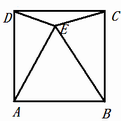

如图，在直角坐标系中，点P₀的坐标为（），将线段OP₀绕点O按逆时针方向旋转45°，再将其长度伸长为OP₀的2倍，得到线段OP₁；又将线段OP₁绕点O按逆时针方向旋转45°，长度伸长为OP₁的2倍，得到线段OP₂；如此下去，得到线段OP₃，OP₄，…，OP_n（n为正整数），则点P₂₀₁₄的坐标是     ．

把边长为1的正方形纸片OABC放在直线m上，OA边在直线m上，然后将正方形纸片绕着顶点A按顺时针方向旋转90°，此时，点O运动到了点O₁处（即点B处），点C运动到了点C₁处，点B运动到了点B₁处，又将正方形纸片AO₁C₁B₁绕B₁点，按顺时针方向旋转90°…，按上述方法经过4次旋转后，顶点O经过的总路程为　　，经过61次旋转后，顶点O经过的总路程为　　．