初中数学二元一次不定方程的应用试题

甲种电影票每张20元，乙种电影票每张15元，若购买甲、乙两种电影票共40张，恰好用去700元，则甲种电影票买了       张．

（满分8分）某校运动会需购买A、B两种奖品．若购买A种奖品3件和B种奖品2件，共需60元；若购买A种奖品5件和B种奖品3件，共需95元．
（1）求A、B两种奖品单价各是多少元？
（2）学校计划购买A、B两种奖品共100件，购买费用不超过1150元，且A种奖品的数量不大于B种奖品数量的3倍．设购买A种奖品m件，购买费用为W元，写出W（元）与m（件）之间的函数关系式，求出自变量m的取值范围，并确定最少费用W的值．

在东营市中小学标准化建设工程中，某学校计划购进一批电脑和电子白板，经过市场考察得知，购买1台电脑和2台电子白板需要3．5万元，购买2台电脑和1台电子白板需要2．5万元．
（1）求每台电脑、每台电子白板各多少万元？
（2）根据学校实际，需购进电脑和电子白板共30台，总费用不超过30万元，但不低于28万元，请你通过计算求出有几种购买方案，哪种方案费用最低．

甲、乙两个牧童，甲对乙说：“把你的样给我一只，我的羊就是你的两倍。”乙回答说：“如果把你的羊给我一只。我们俩的羊数就一样多了。”甲乙原来各有多少只羊？（  ）

A．7,5

B．5，7

C．6,5

D．5,5

某电器商场销售A，B两种型号计算器，两种计算器的进货价格分别为每台30元，40元．商场销售5台A型号和1台B型号计算器，可获利润76元；销售6台A型号和3台B型号计算器，可获利润120元．
（1）求商场销售A，B两种型号计算器的销售价格分别是多少元？（利润=销售价格﹣进货价格）
（2）商场准备用不多于2500元的资金购进A，B两种型号计算器共70台，问最少需要购进A型号的计算器多少台？

用四个完全一样的长方形和一个小正方形拼成如图所示的大长方形的长和宽，已知大正方形的面积是121，小正方形的面积是9，若用x，y（x＞y）表示长方形的长和宽，则下列关系中不正确的是（    ）．

A．x+y=11

B．x^2+y^2=180

C．x﹣y=3

D．x•y=28

某商店销售10台A型和20台B型电脑的利润为4000元，销售20台A型和10台B型电脑的利润为3500元．
（1）求每台A型电脑和B型电脑的销售利润；
（2）该商店计划一次购进两种型号的电脑共100台，其中B型电脑的进货量不超过A型电脑的2倍，设购进A型电脑x台，这100台电脑的销售总利润为y元．
①求y关于x的函数关系式；
②该商店购进A型、B型电脑各多少台，才能使销售总利润最大？
（3）实际进货时，厂家对A型电脑出厂价下调m（0＜m＜100）元，且限定商店最多购进A型电脑70台，若商店保持同种电脑的售价不变，请你根据以上信息及（2）中条件，设计出使这100台电脑销售总利润最大的进货方案．

山地自行车越来越受中学生的喜爱，各种品牌相继投放市场，某车行经营的A型车今年毎辆销售价比去年降低
400元，则今年销售5辆车与去年销售4辆车的销售金额相同．
（1）求该车行今年和去年A型车每辆销售价各多少元？
（2）该车行今年计划进一批A型车和新款B型车共60辆，且B型车的进货数量不超过A型车数量的两倍．若今年A型车进货价毎辆1100元，B型车进货价每辆1600元、销售价每辆2200元．设进A型车a辆，这批车卖完后获得利润W元？应如何进货才能使这批车获得利润最多？

为了研究吸烟是否对肺癌有影响，某肿瘤研究所随机地抽查了10000人，并进行统计分析．结果显示：在吸烟者中患肺癌的比例是2.5%，在不吸烟者中患肺癌的比例是0.5%，吸烟者患肺癌的人数比不吸烟者患肺癌的人数多22人．如果设这10000人中，吸烟者患肺癌的人数为x，不吸烟者患肺癌的人数为y，根据题意，下面列出的方程组正确的是（ ）

A．	B．
C．	D．

一列火车通过一座1000米的大桥需65秒，如果用同样的速度通过一座730米得隧道则要50秒。求这列火车前进的速度和火车的长度。

为打造阜宁老大桥西侧射阳河风光带，现有一段长为350米的河边道路整治任务由A、B两个工程队先后接力完成。A工程队每天整治15米，B工程队每天整治10米，共用时30天。
（1）根据题意，甲、乙两个同学分别列出了尚不完整的方程组如下：
甲：        乙：
根据甲、乙两名同学所列的方程组，请你分别指出未知数x,y表示的意义，然后在方框中补全甲、乙两名同学所列的方程组：
甲：x表示                    ，y表示                   ；
乙：x表示                     ，y表示                   ；
（2）求A、B两工程队分别整治河道多少米？

20位同学在植树节这天共种了52棵树苗，其中男生每人种3棵，女生每人种2棵．设男生有x人，女生有y人，根据题意，列方程组正确的是（   ）

A．	B．
C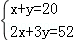．	D．

若方程组的解x、y的和为0，则k的值为  ．

某商店需要购进甲、乙两种商品共160件，其进价和售价如下表：（注：利润=售价-进价）

	甲	乙
进价（元/件）	15	35
售价（元/件）	20	45

若商店计划销售完这批商品后能使利润达到1100元，问甲、乙两种商品应分别购进多少件？

为了抓住集安国际枫叶旅游节的商机，某商店决定购进A、B两种旅游纪念品.若购进A种
纪念品8件，B种纪念品3件，需要950元；若购进A种纪念品5件，B种纪念品6件，
需要800元.
（1）求购进A、B两种纪念品每件各需多少元；
（2）若该商店决定购进这两种纪念品共100件，考虑市场需求和资金周转，用于购买这100
件纪念品的资金不少于7500元，但不超过7650元，那么该商店共有几种进货方案？
（3）若销售每件A种纪念品可获利润20元，每件B种纪念品可获利润30元，在第（2）
问的各种进货方案中，哪一种方案获利最大？最大利润是多少元？