初中数学二元一次不定方程的应用试题

二元一次方程组 的解为（    ）

A．

B．

C．

D．

某木工厂有22人，一个工人每天可加工3张桌子或10只椅子，1张桌子与4只椅子配套，现要求工人每天做的桌子和椅子完整配套而没有剩余，若设安排x个工人加工桌子，y个工人加工椅子，则列出正确的二元一次方程组为（    ）

A．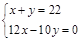

B．

C．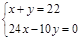

D．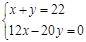

若2x³yⁿ⁺¹与-5x^m-2y²是同类项，则m=     ， n=         ．

已知关于、的方程组的解满足不等式组，求满足条件的的整数值．

某服装店用6000元购进A，B两种新式服装，按标价售出后可获得毛利润3800元（毛利润=售价－进价），这两种服装的进价、标价如下表所示：

类型 价格	A型	B型
进价（元/件）	60	100
标价（元/件）	100	160

 
（1）求这两种服装各购进的件数；
（2）如果A中服装按标价的8折出售，B中服装按标价的7折出售，那么这批服装全部售完后，服装店比按标价售出少收入多少元？

解方程组：

已知是方程组的解，则的值是（  ）

A．－1

B．2

C．3

D．4

阅读下列材料：
解答“已知x﹣y=2，且x＞1，y＜0，试确定x+y的取值范围”有如下解法：
解：∵x﹣y=2，又∵x＞1，∴y+2＞1，即y＞﹣1
又y＜0，∴﹣1＜y＜0．…①
同理得：1＜x＜2．…②
由①+②得﹣1+1＜y+x＜0+2，∴x+y的取值范围是0＜x+y＜2．
请按照上述方法，完成下列问题：
已知关于x、y的方程组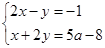的解都为非负数．
（1）求a的取值范围；
（2）已知2a﹣b=1，且，求a+b的取值范围；
（3）已知a﹣b=m（m是大于1的常数），且b≤1，求2a+b最大值．（用含m的代数式表示）

（乐山）“六一”期间，小张购进100只两种型号的文具进行销售，其进价和售价之间的关系如下表：

（1）小张如何进货，使进货款恰好为1300元？
（2）要使销售文具所获利润最大，且所获利润不超过进货价格的40%，请你帮小张设计一个进货方案，并求出其所获利润的最大值．

某服装店用6000元购进A，B两种新式服装，按标价售出后可获得毛利润3800元（毛利润=售价－进价），这两种服装的进价、标价如下表所示：

类型 价格	A型	B型
进价（元/件）	60	100
标价（元/件）	100	160

（1）求这两种服装各购进的件数；
（2）如果A中服装按标价的8折出售，B中服装按标价的7折出售，那么这批服装全部售完后，服装店比按标价售出少收入多少元？

解方程组：

已知是方程组的解，则的值是（ ）

A．－1

B．2

C．3

D．4

四川地震后，某商家为支援灾区人民，计划捐赠帐篷16800顶，该商家备有2辆大货车、8辆小货车运送帐篷．计划大货车比小货车每辆每次多运帐篷200顶，大、小货车每天均运送一次，两天恰好运完．
（1）求大、小货车原计划每辆每次各运送帐篷多少顶？
（2）因地震导致路基受损，实际运送过程中，每辆大货车每次比原计划少运200m顶，每辆小货车每次比原计划少运300m顶，为了尽快将帐篷运送到灾区，大货车每天比原计划多跑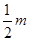次，小货车每天比原计划多跑m次，一天恰好运送了帐篷14400顶，求m的值．

“保护好环境，拒绝冒黑烟”．某市公交公司将淘汰某一条线路上“冒黑烟”较严重的公交车，计划购买A型和B型两种环保节能公交车共10辆，若购买A型公交车1辆，B型公交车2辆，共需400万元；若购买A型公交车2辆，B型公交车1辆，共需350万元．
（1）求购买A型和B型公交车每辆各需多少万元？
（2） 预计在该线路上A型和B型公交车每辆年均载客量分别为60万人次和100万人次．若该公司购买A型和B型公交车的总费用不超过1200万元，且确保这10辆公交车在该线路的年均载客总和不少于680万人次，则该公司有哪几种购车方案？哪种购车方案总费用最少？最少总费用是多少？

甲、乙两个车间工人人数不相等，若甲车间调10人到乙车间，则两车间人数相等；若乙车间调10人到甲车间，则甲车间的人数就是乙车间人数的2倍，求原来甲、乙两车间各有多少名工人？