为支援四川雅安地震灾区,某市民政局组织募捐了240吨救灾物资,现准备租用甲、乙两种货车,将这批救灾物资一次性全部运往灾区,它们的载货量和租金如下表:
| |
甲种货车 |
乙种货车 |
| 载货量(吨/辆) |
45 |
30 |
| 租金(元/辆) |
400 |
300 |
如果计划租用6辆货车,且租车的总费用不超过2300元,求最省钱的租车方案.
某体育用品商场采购员要到厂家批发购进篮球和排球共100只,付款总额不得超过11815元,已知两种球厂家的批发价和商场的零售价如下表,试解答下列问题:
| 品名 |
厂家批发价(元/只) |
市场零售价(元/只) |
| 篮球 |
130 |
160 |
| 排球 |
100 |
120 |
⑴该采购员最多可购进篮球多少只?
⑵若该商场把100只球全部以零售价售出,为使商场的利润不低于2590元,则采购员采购的方案有几种?
纸箱厂用如图1所示的长方形和正方形纸板,做成如图2所示的竖式与横式两种长方体形状的有底无盖纸盒.
(1)现有正方形纸板172张,长方形纸板330张.若要做两种纸盒共l00个,设做竖式纸盒x个.
①根据题意,完成以下表格:
 纸盒 纸盒纸板 |
竖式纸盒(个) |
横式纸盒(个) |
| x |
|
|
| 正方形纸板(张) |
|
2(100-x) |
| 长方形纸板(张) |
4x |
|
②按两种纸盒的数量分,有哪几种生产方案?
(2)若有正方形纸板112张,长方形纸板 张,做成上述两种纸盒,纸板恰好用完.已知100<
张,做成上述两种纸盒,纸板恰好用完.已知100< <110,则
<110,则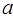 的值是 .
的值是 .
苏州地处太湖之滨,有丰富的水产养殖资源,水产养殖户李大爷准备进行大闸蟹与河虾的混合养殖,他了解到如下信息:
①每亩水面的年租金为500元,水面需按整数亩出租;
②每亩水面可在年初混合投放4公斤蟹苗和20公斤虾苗;
③每公斤蟹苗的价格为75元,其饲养费用为525元,当年可获1400元收益;
④每公斤虾苗的价格为15元,其饲养费用为85元,当年可获160元收益;
(1)若租用水面n亩,则年租金共需 元;
(2)水产养殖的成本包括水面年租金、苗种费用和饲养费用,求每亩水面蟹虾混合养殖的年利润(利润:收益—成本);
(3)李大爷现有资金25000元,他准备再向银行贷不超过25000元的款。用于蟹虾混合养殖。已知银行贷款的年利率为8%,试问李大爷应该租多少亩水面,并向银行贷款多少元.可使年利润超过35000元?
解不等式组 请结合题意填空,完成本题的解答:
请结合题意填空,完成本题的解答:
(Ⅰ)解不等式①,得 ;
(Ⅱ)解不等式②,得 ;
(Ⅲ)把不等式①和②的解集在数轴上表示出来;
(Ⅳ)原不等式组的解集为 .
不等式组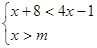 的解集是
的解集是 >3,则m的取值范围是
>3,则m的取值范围是
| A.m=3 | B.m≥3 | C.m≤3 | D.m<3 |
学校计划选购甲、乙两种图书作为“校园读书节”的奖品.已知甲图书的单价是乙图书单价的1.5倍;用600元单独购买甲种图书比单独购买乙种图书要少10本.
(1)甲、乙两种图书的单价分别为多少元?
(2)若学校计划购买这两种图书共40本,且投入的经费不超过1050元,要使购买的甲种图书数量不少于乙种图书的数量,则共有几种购买方案?
(本题10分)若不等式组 的解集是
的解集是 ,
,
(1)求代数式 的值;
的值;
(2)若 ,
, ,
, 为某三角形的三边长,试求
为某三角形的三边长,试求 的值.
的值.
对x,y定义一种新运算T,规定:T(x,y)= (其中a、b均为非零常数),这里等式右边是通常的四则运算,例如:T(0,1)=
(其中a、b均为非零常数),这里等式右边是通常的四则运算,例如:T(0,1)= =b.
=b.
(1)已知T(1,-1)=-2,T(4,2)=1.
①求a,b的值;
②若关于m的不等式组 恰好有3个整数解,求实数p的取值范围;
恰好有3个整数解,求实数p的取值范围;
(2)若T(x,y)=T(y,x)对任意实数x,y都成立(这里T(x,y)和T(y,x)均有意义),则a,b应满足怎样的关系式?
对x,y定义一种新运算T,规定:T(x,y)=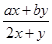 (其中a、b均为非零常数),这里等式右边是通常的四则运算,例如:T(0,1)=
(其中a、b均为非零常数),这里等式右边是通常的四则运算,例如:T(0,1)= =b.
=b.
(1)已知T(1,-1)=-2,T(4,2)=1.
①求a,b的值;
②若关于m的不等式组 恰好有3个整数解,求实数p的取值范围;
恰好有3个整数解,求实数p的取值范围;
(2)若T(x,y)=T(y,x)对任意实数x,y都成立(这里T(x,y)和T(y,x)均有意义),则a,b应满足怎样的关系式?
试题篮
()