阅读下列材料:小华遇到这样一个问题:已知:如图1,在△ABC中,AB=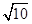 ,AC=
,AC= ,BC=2三边的长分别为,求∠A的正切值.
,BC=2三边的长分别为,求∠A的正切值.
小华是这样解决问题的:如图2所示,先在一个正方形网格(每个小正方形的边长均为1)中画出格点△ABC(△ABC三个顶点都在小正方形的顶点处),然后在这个正方形网格中再画一个和△ABC相似的格点△DEF,从而使问题得解.
(1)图2中与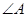 相等的角为 ,
相等的角为 , 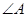 的正切值为 ;
的正切值为 ;
(2)参考小华解决问题的方法,利用图4中的正方形网格(每个小正方形的边长均为1)解决问题:如图3,在△GHK中,HK=2,HG=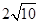 ,KG=
,KG=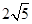 ,延长HK,求
,延长HK,求 的度数.
的度数. 
已知梯形ABCD,请使用无刻度直尺画图.
(1)在图1中画出一个与梯形ABCD面积相等,且以CD为边的三角形;
(2)图2中画一个与梯形ABCD面积相等,且以AB为边的平行四边形.
如果反比例函数 的图象经过点(-1,-2),则k的值是( )
的图象经过点(-1,-2),则k的值是( )
| A.2 | B.-2 | C.-3 | D.3 |
有20个同学排成一行,若从左往右隔1人报数,小李报8号;若从右往左隔2人报数,小陈报6号.那么,从小陈开始向小李逐人报数,小李报的号数为( ).
| A.ll | B.12 | C.13 | D.14 |
下列图形中,单独选用一种图形不能进行平面镶嵌的是
| A.正三角形 | B.正六边形 | C.正方形 | D.正五边形 |
认真观察下图的四个图中阴影部分构成的图案,回答下列问题:
(1)利用所学知识,请写出这四个图案都具有的特征: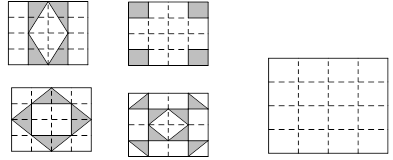
特征1:______________________________________;
特征2:______________________________________;
(2)请在备用图中设计你心目中最美丽的图案,使它也具备你所写的上述
特征.
将一张长与宽的比为2∶1的长方形纸片按如图①、②所示的方式对折,然后沿图③中的虚线裁剪,得到图④,最后将图④的纸片再展开铺平,则所得到的图案是( )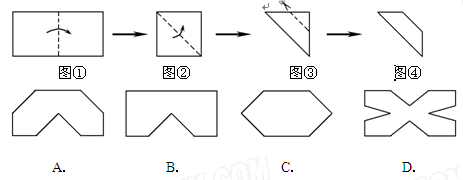
右边的图案是由下面五种基本图形中的两种拼接而成,这两种基本图形是
| A.②⑤ | B.②④ | C.③⑤ | D.①⑤ |
网格中有一个小甲虫( ),它喜欢吃牛粪,它又会把吃剩的牛粪滚成牛粪球(
),它喜欢吃牛粪,它又会把吃剩的牛粪滚成牛粪球( )藏进仓库(
)藏进仓库( ).规定向左为L,向右为R,向上为U,向下D,如:L1表示向左平移一格,D2表示向下平移2格.例如:要把左图中的所有的牛粪球推到最近的仓库里,可以编写程序:L1-R1-U2-D3-R2-U1,小甲虫就能把所有的牛粪球推到最近的仓库.你来试一试,可编写一个怎样的程序才能使小甲虫把右边图上的所有牛粪球推到最近的仓库里.(只需写出一种可行的程序即可)
).规定向左为L,向右为R,向上为U,向下D,如:L1表示向左平移一格,D2表示向下平移2格.例如:要把左图中的所有的牛粪球推到最近的仓库里,可以编写程序:L1-R1-U2-D3-R2-U1,小甲虫就能把所有的牛粪球推到最近的仓库.你来试一试,可编写一个怎样的程序才能使小甲虫把右边图上的所有牛粪球推到最近的仓库里.(只需写出一种可行的程序即可)

问题:如图1,在正方形ABCD内有一点P,PA= ,PB=
,PB= ,PC=1,求∠BPC的角度.
,PC=1,求∠BPC的角度.
分析:根据已知条件比较分散的特点,我们可以通过旋转变换,将分散的已知条件集中在一起,于是将△BPC绕点B逆时针旋转900,得到了△BP1A(如图2),然后连接PP1.
解决问题:请你通过计算求出图2中∠BPC的角度;
类比研究:如图3,若在正六边形ABCDEF内有一点P,且PA= ,PB=4,PC=2.
,PB=4,PC=2.
(1)请你通过计算求出∠BPC的度数;
(2)直接写出正六边形ABCDEF的边长为 .
已知梯形 中,
中, ∥
∥ ,
, ,
, ,
, ,
, .动点
.动点 从
从 点开始以
点开始以 的速度沿线段
的速度沿线段 向
向 点运动,动点
点运动,动点 从点
从点 开始以
开始以 的速度沿线段
的速度沿线段 向
向 点运动.点
点运动.点 、点
、点 分别从
分别从 、
、 两点同时出发,当其中一点停止时,另一点也随之停止。设运动时间为
两点同时出发,当其中一点停止时,另一点也随之停止。设运动时间为 .
.
(1)求 的长;
的长;
(2)以 为圆心、
为圆心、 长为半径的
长为半径的 与直线
与直线 相切时,求
相切时,求 的值;
的值;
(3)是否存在 的值,使得以
的值,使得以 为圆心、
为圆心、 长为半径的
长为半径的 与以
与以 为圆心、
为圆心、 长为半径的
长为半径的 相切?若存在,求出
相切?若存在,求出 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
试题篮
()