初中数学应用类问题填空题

如图，是一种“羊头”形图案，其作法是：从正方形①开始，以它的一边为斜边，向外作等腰直角三角形，然后再以其直角边为边，分别向外作正方形②和②ˊ，…，依此类推，若正方形①的边长为16cm，则正方形⑦的边长为     ■      。

古希腊数学家把数1，3，6，10，15，21，…，叫做三角形数，它有一定的规律性，则第24个三角形数与第22个三角形数的差为           。

晚上，小亮走在大街上．他发现：当他站在大街两边的两盏路灯之间，并且自己被两边路灯照在地上的两个影子成一直线时，自己右边的影子长为3米，左边的影子长为1.5米．又知自己身高1.80米，两盏路灯的高相同，两盏路灯之间的距离为12米，则路灯的高为　　　　米．

观察下表，回答问题：

第       个图形中“△”的个数是“○”的个数的5倍．

下面是按一定规律排列的一列数，那么第n个数是______．

小宏准备用50元钱买甲、乙两种饮料共10瓶．已知甲饮料每瓶7元，乙饮料每瓶4元，则小宏最多能买          瓶甲饮料．

1883年，康托尔构造的这个分形，称做康托尔集．从数轴上单位长度线段开始，康托尔取走其中间三分之一而达到第一阶段；然后从每一个余下的三分之一线段中取走其中间三分之一而达到第二阶段．无限地重复这一过程，余下的无穷点集就称做康托尔集．上图是康托尔集的最初几个阶段，当达到第八个阶段时，余下的所有线段的长度之和为　　　　．

观察下列各式:
1×3+1=4=2²， 2×4+1=9=3²， 3×5+1=16=4²，4×6+1=25=5²，
…….
请将你所发现的规律用含字母n的式子表示出来:________;

如图，修建一段高速公路时，从甲地测得其走向是北偏东72°，现在甲、乙同时开工，为了准确接通，乙地的施工方向为_____________.

下面共有四种情景：
A. 一辆汽车在公路上匀速行驶（汽车行驶的路程与时间的关系）；
B. 从树上开始往下掉的苹果（苹果落地前的高度与下落时间的关系）；
C. 一杯越来越凉的开水（水温与时间的关系）；
D. 竖直向上抛出的篮球（篮球落地前的速度与时间的关系）；
上面各种情景可以近似的用下面那个图象来表示（横轴表示时间，纵轴表示相应的因变量），A、B、C、D各情景对应的图象依次为：___________。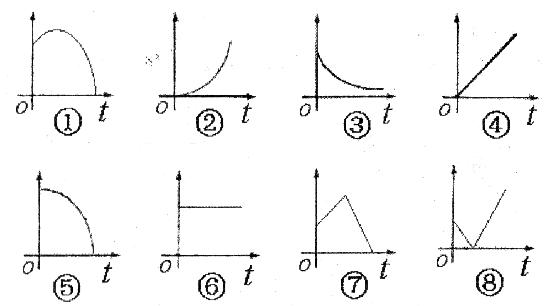

如图，是一个数值转换机.若输入数为3，则输出数是______.

甲乙两人骑摩托车同时从地出发前往地，且两人到达地后各自按原速度返回，且不停地在之间往返行驶，甲的速度为32，乙的速度为18，当乙车由至多次后，甲车两次追上乙车，且第二次追上乙时是在乙车从地向地行驶的途中，且他们此时距地的距离为10，则两地相距__________．

如图中，每个图形都是若干个棋子围成的正方形图案，图案的每条边（包括两个顶点）上都有n（n≤2）个棋子，每个图案的棋子总数为S，按图的排列规律推断S与n之间的关系可以用式子___________来表示． 

△ABC中，已知点D在边BC上，且BD=2DC，设=，=，则等于            .

如图，△ABC中，AB=BC=CA=8．一电子跳蚤开始时在BC边的P₀处，BP₀=3．跳蚤第一步从P₀跳到AC边的P₁（第1次落点）处，且CP₁=CP₀；第二步从P₁跳到AB边的P₂（第2次落点）处，且AP₂=AP₁；第三步从P₂跳到BC边的P₃（第3次落点）处，且BP₃=BP₂；跳蚤按照上述规则一直跳下去，第n次落点为P_n（n为正整数），则点P₂₀₁₂与点P₂₀₁₃之间的距离为 ．