初中数学应用类问题填空题

一串有趣的图案按一定的规律排列(如图)：

 
按此规律在右边的圆中画出的第2011个图案：       。

观察下面的一列数：，－，，－……
请你找出其中排列的规律，并按此规律填空，第9个数是________，第14个数是________．

从边长为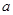的大正方形纸板中挖去一个边长为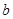的小正方形纸板后，将其裁成四个相同的等腰梯形（图甲），然后拼成一个平行四边形（图乙）．那么通过计算两个图形阴影部分的面积，可以验证成立的公式是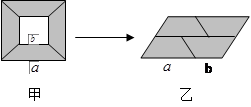

在日常生活中如取款、上网等都需要密码。有一种“因式分解”法产生的密码，方便记忆。原理是：如对于多项式x⁴-y⁴，因式分解的结果是(x-y)(x+y)(x²+y²)，若取x=9,y=9时，则各个因式的值是：x-y=0，(x+y)=18，(x²+y²)=162，于是，就可以把“018162”作为一个六位数的密码。对于多项式4x³-xy²，取x=10,y=10时，用上述方法产生的密码是：_____（写出一个可）。

正方形网格中，每个小正方形的边长为1．图1所示的矩形是由4个全等的直角
梯形拼接而成的（图形的各顶点都在格点上；拼接时图形互不重叠，不留空隙），如果用这
4个直角梯形拼接成一个等腰梯形，那么（1）仿照图1，在图2中画出一个拼接成的等腰梯
形；（2）这个拼接成的等腰梯形的周长为________．

一个圆锥的侧面展开图是半径为1的半圆，则该圆锥的底面半径是   

下面是按一定规律排列的一列数，那么第n个数是______．

、阅读下列材料并填空。平面上有n个点（n≥2）且任意三个点不在同一条直线上，过这些点作直线，一共能作出多少条不同的直线？
①分析：当仅有两个点时，可连成1条直线；当有3个点时，可连成3条直线；当有4个点时，可连成6条直线；当有5个点时，可连成10条直线……
②归纳：考察点的个数和可连成直线的条数发现：如下表

点的个数	可作出直线条数
2	1=
3	3=
4	6=
5	10=
……	……
n

③推理：平面上有n个点，两点确定一条直线。取第一个点A有n种取法，取第二个点B有（n－1）种取法，所以一共可连成n(n-1)条直线，但AB与BA是同一条直线，故应除以2；即
④结论：
试探究以下几个问题：平面上有n个点（n≥3），任意三个点不在同一条直线上，过任意三个点作三角形，一共能作出多少不同的三角形？
（1）分析：
当仅有3个点时，可作出      个三角形；
当仅有4个点时，可作出      个三角形；
当仅有5个点时，可作出      个三角形；
……
（2）归纳：考察点的个数n和可作出的三角形的个数，发现：（填下表）

点的个数	可连成三角形个数
3
4
5
……
n

 
(3)推理：                             
（4）结论：

如图，物理学家在对原子结构研究中，在一个宽的矩形粒子加速器中，一中子从点（点在长边上）出发沿虚线射向边，然后反弹到边上的点. 如果，.那么点与点的距离为             。

如图，小明从点A出发，沿直线前进20m后向左转30⁰，再沿直线前进20m，又向左转30⁰……照这样走下去，小明第一次回到出发点A，一共走了  __    米。

一辆汽车在行驶过程中，路程 （千米）与时间 （小时）之间的函数关系如图3所示 当时 0≤x≤1，关于的函数解析式为，那么当 1≤≤2时，y关于x的函数解析式为______________ .

某校准备召开一次学生代表会，七（1）班有5个参会名额，其中男生必须有m人，于是七（1）班班主任确定从9名（5男4女，其中班长吴英为女生）候选人员中选取.若“选到吴英”的可能性是大于0但小于1，则m=                             .

如图，图①是一块边长为1，周长记为P₁的等边三角形纸板，沿图①的底边剪去一块边长的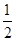 的等边三角形纸板后得到图②，然后沿同一底边依次剪去一块更小的等边三角形纸板（即其边长为前一块被剪掉等边三角形纸板边长的 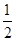）后，得图③，④，…，记第n（n≥3）块纸板的周长为P_n，则P_n-P_n-1=_________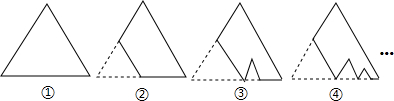  

将一些相同的小三角形按下图所示的规律摆放，请仔细观察，第 n个图形有            个小三角形.（用含 n 的代数式表示）

观察图中每一个大三角形中白色三角形的排列规律，
则第5个大三角形中白色三角形有            个 ．