初中数学应用类问题试题

【原创】（本小题满分6分）
能否在图中的四个圆圈内填入4个互不相同的数，使得任意两个圆圈中所填的数的平方和等于另外两个圆圈中所填数的平方和？如果能填，请填出一个例；如果不能填，请说明理由。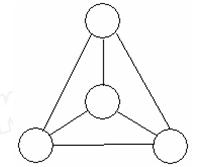

某校对该校七年级（1）班全体学生的血型做了一次全面调查，根据调查结果绘制了下列两幅不完整的统计图，请你根据统计图提供的信息解答以下问题：

（1）该校七年级（1）班有多少名学生．
（2）求出扇形统计图中“O型”血所对扇形的圆心角的度数．
（3）将条形统计图中“B型”血部分的条形图补充完整．

白天的温度是8℃，夜间下降了t℃，则夜间的温度是　　　   　　℃。

一辆汽车装满货物的卡车，2.5m的高，1.6m的宽，要进厂门形状如图某工厂，问这辆卡车能否通过门？请说明理由。

如图，小明同学用自制的直角三角形纸板DEF测量树的高度AB，他调整自己的位置，设法使斜边DF保持水平，并且边DE与点B在同一直线上．已知纸板的两条直角边DF=50cm，EF=30cm，测得边DF离地面的高度AC=1.5m，CD=20m，则树高AB为（   ）

A．12 m

B．13.5 m

C．15 m

D．16.5 m

. 如图，是小刚在电脑中设计的一个电子跳蚤，每跳一次包括上升和下降，即由点A—B—C为一个完整的动作。按照图中的规律，如果这个电子跳蚤落到9的位置，它需要跳的次数为          

A．5次

B．6次

C．7次

D．8次（　）

电焊工想利用一块边长为的正方形钢板做成一个扇形，于是设计了以下三种方案：
方案一：如图1，直接从钢板上割下扇形．
方案二：如图2，先在钢板上沿对角线割下两个扇形，再焊接成一个大扇形（如图3）．
方案三：如图4，先把钢板分成两个相同的小矩形，并在每个小矩形里割下两个小扇形，然后将四个小扇形按与图3类似的方法焊接成一个大扇形．

图1                图2               图3                图4
（1）容易得出图1、图3中所得扇形的圆心角均为，那么按方案三所焊接成的大扇形的圆心角也为吗？为什么？
（2）容易得出图1中扇形与图3中所得大扇形的面积相等，那么按方案三所焊成的大扇形的面积也与方案二所焊接成的大扇形的面积相等吗？若不相等，面积是增大还是减小？为什么？
（3）若将正方形钢板按类似图4的方式割成个相同的小矩形，并在每个小矩形里割下两个小扇形，然后将这个小扇形按类似方案三的方式焊接成一个大扇形，则当逐渐增大时，所焊接成的大扇形的面积如何变化？

问题背景 某课外学习小组在一次学习研讨中，得到如下两个命题：
①  如图1，O是正三角形ABC的中心，∠MON分别与AB、BC交于点P,Q，若∠MON = 120°，则四边形OPBQ的面积等于三角形ABC面积的三分之一.
②  如图2，O是正方形ABCD的中心，∠MON分别与AB、BC交于点P,Q，若∠MON = 90°，则四边形OPBQ的面积等于正方形ABCD面积的四分之一.然后运用类比的思想提出了如下的命题：
③  如图3，O是正五边形ABCDE的中心，∠MON分别与AB、BC交于点P,Q，若∠MON = 72°，则四边形OPBQ的面积等于五边形ABCDE面积的五分之一.
、任务要求 
（1）请你从①、②、③三个命题中选择一个进行证明；（说明：选①做对的得5分，选②做对的得4分，选③做对的得6分）
（2）请你继续完成下面的探索：
如图④，在正n（n≥3）边形ABCDEF…中，O是中心,∠MON分别与AB、BC交于点P,Q，若∠MON等于多少度时，则四边形OPBQ的面积等于正n边形ABCDE…面积的n分之一？（不要求证明）
解：（1）我选            .
证明：

如图所示，把一张矩形纸片对折，折痕为AB，再把以AB的中点O为顶点的平角∠AOB三等分，沿平角的三等分线折叠，将折叠后的图形剪出一个以O为顶点的等腰三角形，那么剪出的等腰三角形全部展开平铺后得到的平面图形一定是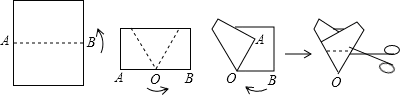

A．正三角形

B．正方形

C．正五边形

D．正六边形

小明沿着坡比为1：的山坡向上走了600m，则他升高了（    ）

A．m

B．200m

C．300 m

D．200m

对四堆石子进行如下“操作”：每次允许从每堆中各拿掉相同个数的石子，或从任一堆中取出
一些石子放入另一堆中。若四堆石子的个数分别为2011，2010，2009，2008，则按上述方式
进行若干次“操作”后，四堆石子的个数可能是(      )。

A．0, 0, 0, 1

B．0, 0, 0, 2

C．0, 0, 0, 3

D．0, 0, 0, 4 。

问题再现
现实生活中，镶嵌图案在地面、墙面乃至于服装面料设计中随处可见．在八年级课题学习“平面图形的镶嵌”中，对于单种多边形的镶嵌，主要研究了三角形、四边形、正六边形的镶嵌问题．今天我们把正多边形的镶嵌作为研究问题的切入点，提出其中几个问题，共同来探究.

我们知道，可以单独用正三角形、正方形或正六边形镶嵌平面．如右图中，用正方形镶嵌平面，可以发现在一个顶点O周围围绕着4个正方形的内角.
试想：如果用正六边形来镶嵌平面，在一个顶点周围应该围绕着         个
正六边形的内角．
问题提出
如果我们要同时用两种不同的正多边形镶嵌平面，可能设计出几种不同的组合方案？
问题解决
猜想1：是否可以同时用正方形、正八边形两种正多边形组合进行平面镶嵌？
分析：我们可以将此问题转化为数学问题来解决．从平面图形的镶嵌中可以发现，解决问题的关键在于分析能同时用于完整镶嵌平面的两种正多边形的内角特点．具体地说，就是在镶嵌平面时，一个顶点周围围绕的各个正多边形的内角恰好拼成一个周角．
验证1：在镶嵌平面时，设围绕某一点有x个正方形和y个正八边形的内角可以拼成一个周角．根据题意，可得方程：
，整理得：，
我们可以找到惟一一组适合方程的正整数解为 ．  
结论1：镶嵌平面时，在一个顶点周围围绕着1个正方形和2个正八边形的内角可以拼成一个周角，所以同时用正方形和正八边形两种正多边形组合可以进行平面镶嵌．
猜想2：是否可以同时用正三角形和正六边形两种正多边形组合进行平面镶嵌？若能，请按照上述方法进行验证，并写出所有可能的方案；若不能，请说明理由．
验证2：
结论2：                                                                     
                                                                              
上面，我们探究了同时用两种不同的正多边形组合镶嵌平面的部分情况，仅仅得到了一部分组合方案，相信同学们用同样的方法，一定会找到其它可能的组合方案．
问题拓广
请你仿照上面的研究方式，探索出一个同时用三种不同的正多边形组合进行平面镶嵌的方案，并写出验证过程．
猜想3：                                                                     .
验证3：
结论3：                                                                     
                                                                                .

观察图中每一个大三角形中白色三角形的排列规律，
则第5个大三角形中白色三角形有            个 ．

在平面上有且只有4个点，这4个点中有一个独特的性质：连结每两点可得到6条线段，这6条线段有且只有两种长度．我们把这四个点称作准等距点．例如正方形ABCD的四个顶点(如图1)，有AB=BC=CD=DA，AC=BD．其实满足这样性质的图形有很多，如图2中A、B、C、O四个点，满足AB=BC=CA，OA=OB=OC；如图3中A、B、C、O四个点，满足OA=OB=OC=BC，AB=AC．


（1）如图，若等腰梯形ABCD的四个顶点是准等距点，且AD∥BC．
①写出相等的线段（不再添加字母）；
②求∠BCD的度数．
（2）请再画出一个四边形，使它的四个顶点为准等距点，并写出相等的线段．

如图，一轮船由B处向C处航行，在B处测得C处在B的北偏东75°方向上，在海岛上的观察所A测得B在A的南偏西30°方向上，C在A的南偏东25°方向。若轮船行驶到C处，那么从C处看A，B两处的视角∠ACB是多少度？