初中数学应用类问题试题

某初中学校共有学生720人，该校有关部门从全体学生中随机抽取了50人，对其到校方式进行调查，并将调查的结果制成了如图所示的条形统计图，由此可以估计全校坐公交车到校的学生有  人．

如图1，△ABC中，AB=AC=5cm，BC=6cm，边长为2cm的菱形DEFG两边DG、DE分别在AC、AB上．若菱形DEFG以1cm/s的速度沿射线AC方向平移．
（1）经过  ▲  秒菱形DEFG的顶点F恰好在BC上；
（2）求菱形DEFG的面积；
（3）设菱形DEFG与△ABC的重合部分为Scm²，菱形DEFG平移的时间为t秒．求S与t的函数关系式．

（8分）A、B两地相距630千米，客车、货车分别从A、B两地同时出发，匀速相向行驶．货车两小时可到达途中C站，客车需9小时到达C站（如图1所示）．货车的速度是客车的 ，客、货车到C站的距离分别为y₁、y₂（千米），它们与行驶时间x（小
时）之间的函数关系如图2所示．

（1）求客、货两车的速度；
（2）求两小时后，货车到C站的距离y₂与行驶时间x之间的函数关系式；
（3）如图2，两函数图象交于点E，求E点坐标，并说明它所表示的实际意义．

甲、乙、丙、丁四人进行射击测试,每人10次射击的平均成绩恰好都是9.4环,
方差分别是,,,.在本次射击测试中,成绩最
稳定的是

A．甲

B．乙

C．丙

D．丁

（本小题满分10分）如图1，点C将线段AB分成两部分，如果AB : AC="AC" : BC，那么称点C为线段的黄金分割点．某研究小组在进行课题学习时，由黄金分割点联想到“黄金分割线”，类似地给出“黄金分割线”的定义：直线将一个面积为S的图形分成两部分，这两部分的面积分别为S₁: S₂，如果S : S₁= S₁: S₂，，那么称直线为该图形的黄金分割线．
（1）研究小组猜想：在△ABC中，若点D为AB边上的黄金分割点（如图2），则直线CD是△ABC的黄金分割线．你认为对吗？为什么？
（2）请你说明：三角形的中线是否也是该三角形的黄金分割线？
（3）研究小组探究发现：在（1）中，过点C任作AE交AB于E，再过点D作，交 AC于点F，连接EF（如图3），则直线EF是△ABC的黄金分割线．请说明理由．
（4）如图4，点E是ABCD的边AB的黄金分割点，过点E作，交DC于点F，显然直线EF是ABCD的黄金分割线．请你再画一条ABCD的黄金分割线，使它不经过ABCD各边黄金分割点（保留必要的辅助线）．

（11·贺州）
某生姜种植基地计划种植A、B两种生姜30亩．已知A、B两种生姜的年产量分别为2 000千克/亩、2 500千克/亩，收购单价分别是8元/千克、7元/千克．
（1）若该基地收获两种生姜的年总产量为68 000千克，求A、B两种生姜各种多少亩？
（2）若要求种植A种生姜的亩数不少于B种的一半，那么种植A、B两种生姜各多少亩时，
全部收购该基地生姜的年总收入最多？最多是多少元？

长为1，宽为a的矩形纸片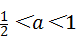（），如图那样折一下，剪下一个边长等于矩形宽度的正方形（称为第一次操作）；再把剩下的矩形如图那样折一下，剪下一个边长等于此时矩形宽度的正方形（称为第二次操作）；如此反复操作下去．若在第n此操作后，剩下的矩形为正方形，则操作终止．当n=3时，a的值为（ ）

图1是一个边长为1的等边三角形和一个菱形的组合图形，菱形边长为等边三角形边长的一半，以此为基本单位，可以拼成一个形状相同但尺寸更大的图形（如图2），依此规律继续拼下去（如图3），…，则第n个图形的周长是（　　）

A．2^n	B．4^n
C．2^n+1	D．2^n+2

随机从甲、乙两块试验田中各抽取100株麦苗测量高度，计算平均数和方差的结果为：，，，，则小麦长势比较整齐的试验田是   (填“甲”或“乙”)

如图9，给正五边形的顶点依次编号为1，2，3，4，5.若从某一顶点开始，沿正五边形的边顺时针行走，顶点编号的数字是几，就走几个边长，则称这种走法为一次“移位”.
如：小宇在编号为3的顶点时，那么他应走3个边长，即从3→4→5→1为第一次“移位”，这时他到达编号为1的顶点；然后从1→2为第二次“移位”.若小宇从编号为2的顶点开始，第10次“移位”后，则他所处顶点的编号是____________.

△ABC是一张等腰直角三角形纸板，∠C=Rt∠，AC=BC=2，
（1）要在这张纸板中剪出一个尽可能大的正方形，有甲、乙两种剪法（如图1），比较甲、乙两种剪法，哪种剪法所得的正方形面积大？请说明理由．
（2）图1中甲种剪法称为第1次剪取，记所得正方形面积为s₁；按照甲种剪法，在余下的△ADE和△BDF中，分别剪取正方形，得到两个相同的正方形，称为第2次剪取，并记这两个正方形面积和为s₂（如图2），则s₂=；再在余下的四个三角形中，用同样方法分别剪取正方形，得到四个相同的正方形，称为第3次剪取，并记这四个正方形面积和为s₃，继续操作下去…，则第10次剪取时，s₁₀=；
（3）求第10次剪取后，余下的所有小三角形的面积之和．

图为手的示意图，在各个手指间标记A,B,C,D请你按图中箭头所指方向（A→B→C→D→C→B→A→B→C→ 的方式），从A开始数连续正整数1,2,3,4 当数到2011时，其对应的字母是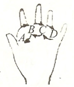

A．A

B．B

C． C

D．D

一个边长为16m的正方形展厅，准备用边长分别为1m和0.5m的两种正方形地
板砖铺设其地面．要求正中心一块是边长为1m的大地板砖，然后从内到外一圈小地板砖、
一圈大地板砖相间镶嵌（如图所示），则铺好整个展厅地面共需要边长为1m的大地板砖   
块．

下列判断正确的有（　　）
①顺次连接对角线互相垂直且相等的四边形的各边中点一定构成正方形；
②中心投影的投影线彼此平行；
③在周长为定值π的扇形中，当半径为时扇形的面积最大；
④相等的角是对顶角的逆命题是真命题．

A．4个	B．3个
C．2个	D．1个

一种电讯信号转发装置的发射直径为31km．现要求：在一边长为30km的正方形城区选择若干个安装点，每个点安装一个这种转发装置，使这些装置转发的信号能完全覆盖这个城市．问：
（1）能否找到这样的4个安装点，使得这些点安装了这种转发装置后能达到预设的要求？
（2）至少需要选择多少个安装点，才能使这些点安装了这种转发装置后达到预设的要求？
答题要求：请你在解答时，画出必要的示意图，并用必要的计算、推理和文字来说明你的理由．（下面给出了几个边长为30km的正方形城区示意图，供解题时选用）

图1               图2                  图3                图4