已知x1,x2是一元二次方程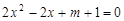 的两个实数根.
的两个实数根.
(1)求实数m的取值范围;
(2)如果x1,x2满足不等式 ,且m为整数,求m的值.
,且m为整数,求m的值.
菱形ABCD的对角线AC,BD相交于点O, .动点P在线段BD上从点B向点D运动,PF⊥AB于点F,四边形PFBG关于BD对称,四边形QEDH与四边形PFBG关于AC对称.设菱形ABCD被这两个四边形盖住部分的面积为
.动点P在线段BD上从点B向点D运动,PF⊥AB于点F,四边形PFBG关于BD对称,四边形QEDH与四边形PFBG关于AC对称.设菱形ABCD被这两个四边形盖住部分的面积为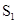 ,未盖住部分的面积为
,未盖住部分的面积为 ,
, .
.
(1)用含x代数式分别表示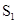 ,
, ;
;
(2)若 ,求x.
,求x.
如图,在直角梯形ABCD中,AB∥CD,∠BCD=Rt∠,AB=AD=10cm,BC=8cm.点P从点A出发,以每秒3cm的速度沿折线ABCD方向运动,点Q从点D出发,以每秒2cm的速度沿线段DC方向向点C运动.已知动点P、Q同时发,当点Q运动到点C时,P、Q运动停止,设运动时间为t.
(1)求CD的长;
(2)当四边形PBQD为平行四边形时,求四边形PBQD的周长;
(3)在点P、点Q的运动过程中,是否存在某一时刻,使得△BPQ的面积为20cm2?若存在,请求出所有满足条件的t的值;若不存在,请说明理由.
在直角坐标系中,A(0,4),B(4 ,0).点C从点B出发沿BA方向以每秒2个单位的速度向点A匀速运动,同时点D从点A出发沿AO方向以每秒1个单位的速度向点O匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点C、D运动的时间是t秒(t>0).过点C作CE⊥BO于点E,连结CD、DE.
,0).点C从点B出发沿BA方向以每秒2个单位的速度向点A匀速运动,同时点D从点A出发沿AO方向以每秒1个单位的速度向点O匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点C、D运动的时间是t秒(t>0).过点C作CE⊥BO于点E,连结CD、DE.
⑴ 当t为何值时,线段CD的长为4;
⑵ 当线段DE与以点O为圆心,半径为 的⊙O有两个公共交点时,求t的取值范围;
的⊙O有两个公共交点时,求t的取值范围;
⑶ 当t为何值时,以C为圆心、CB为半径的⊙C与⑵中的⊙O相切?
如图,△AEF中,∠EAF=45°,AG⊥EF于点G,现将△AEG沿AE折叠得到△AEB,将△AFG沿AF折叠得到△AFD,延长BE和DF相交于点C.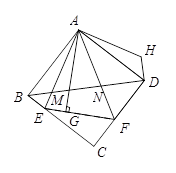
(1)求证:四边形ABCD是正方形;
(2)连接BD分别交AE、AF于点M、N,将△ABM绕点A逆时针旋转,使AB与AD重合,得到△ADH,试判断线段MN、ND、DH之间的数量关系,并说明理由.
(3)若EG=4,GF=6,BM=3,求AG、MN的长.
如图,梯形ABCD中,AB∥CD,∠ABC=90°,AB=8,CD=6,BC=4,AB边上有一动点P(不与A、B重合),连结DP,作PQ⊥DP,使得PQ交射线BC于点E,设AP=x.


⑴当x为何值时,△APD是等腰三角形?
⑵若设BE=y,求y关于x的函数关系式;
⑶若BC的长可以变化,在现在的条件下,是否存在点P,使得PQ经过点C?若存在,求出相应的AP的长;若不存在,请说明理由,并直接写出当BC的长在什么范围内时,可以存在这样的点P,使得PQ经过点C.
商场某种商品平均每天可销售30件,每件盈利50元.为了尽快减少库存,商场决定采取适当的降价措施.经调查发现,每件商品每降价1元,商场平均每天可多售出2件.设每件商品降价x元.据此规律,请回答:
(1)商场日销售量增加 件,每件商品盈利 元(用含x的代数式表示);
(2)在上述条件不变、销售正常情况下,每件商品降价多少元时,商场日盈利可达到2100元?
已知关于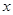 的一元二次方程
的一元二次方程 .
.
(1)求证:当 取不等于l的实数时,此方程总有两个实数根.
取不等于l的实数时,此方程总有两个实数根.
(2)若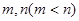 是此方程的两根,并且
是此方程的两根,并且 ,直线
,直线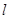 :
: 交
交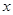 轴于点A,交
轴于点A,交 轴于点B,坐标原点O关于直线
轴于点B,坐标原点O关于直线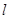 的对称点O′在反比例函数
的对称点O′在反比例函数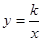 的图象上,求反比例函数
的图象上,求反比例函数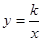 的解析式.
的解析式.
(3)在(2)的成立的条件下,将直线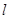 绕点A逆时针旋转角
绕点A逆时针旋转角 ,得到直线
,得到直线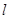 ′,
′,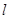 ′交
′交 轴于点P,过点P作
轴于点P,过点P作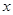 轴的平行线,与上述反比例函数
轴的平行线,与上述反比例函数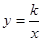 的图象交于点Q,当四边形APQO′的面积为
的图象交于点Q,当四边形APQO′的面积为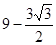 时,求角
时,求角 的值.
的值.
如图,在△ABC中,AB=AC=13厘米,BC=10厘米,AD⊥BC于点D,动点P从点A出发以每秒1厘米的速度在线段AD上向终点D运动。设动点运动时间为t秒。
(1)求AD的长.
(2)当△PDC的面积为15平方厘米时,求 的值.
的值.
(3)动点M从点C出发以每秒2厘米的速度在线段CB上运动.点M与点P同时出发,且当点P运动到终点D时,点M也停止运动。是否存在t,使得S△PMD= S△ABC?若存在,请求出t的值;若不存在,请说明理由.
S△ABC?若存在,请求出t的值;若不存在,请说明理由.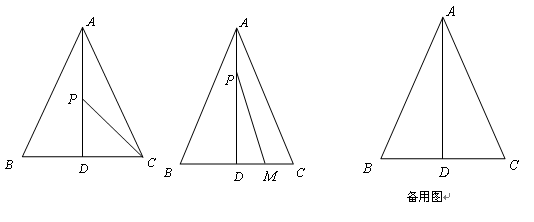
试题篮
()