初中数学一元二次方程的最值选择题

已知关于x的方程x²-（m-2）x+m²=0有两个相等的实数根，则方程的根为（   ）

A．x1=x2="1"

B．x1=x2="-2"

C．x1=x2="-1"

D．x1=x2=2

一元二次方程x²+2=0的根的情况为（   ）

A．没有实根	B．有两个相等的实根
C．有两个不等的实根	D．有两个实根

用配方法解方程x²-2x-5=0时，原方程应变形为（ ）

A．（x+1）^2=6

B．（x+2）^2=9

C．（x-1）^2="6"

D．（x-2）^2=9

若关于x的一元二次方程kx²-2x+1=0有实数根，则k的取值范围是（ ）

A．k＜1

B．k≤1

C．k＜1且k≠0

D．k≤1且k≠0

方程2x（x+3）=0的根的情况是（ ）

A．有两个不相等的实数根	B．有两个相等的实数根
C．只有一个实数根	D．没有实数根

用配方法把一元二次方程x²+6x+1=0，配成（x+p）²=q的形式，其结果是（ ）

A．（x+3）^2=8	B．（x﹣3）^2=1
C．（x﹣3）^2=10	D．（x+3）^2=4

若x=1是一元二次方程（x+1）²﹣a（x+1）﹣2=0的一个根，则a的值是（ ）．

A．﹣2

B．﹣1

C．1

D．2

关于x的方程x²-2x+k=0有两个不相等的实数根，则k的取值范围是（      ）

A．k＜1

B．k＞1

C．k＜-1

D．k＞-1

用配方法解一元二次方程x²+4x-5=0，此方程可变形为（   ）

A．（x+2）^2="9"

B．（x-2）^2="9"

C．（x+2）^2="1"

D．（x-2）^2=1

一元二次方程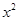+x+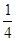=0的根的情况是（ ）

A．有两个不相等的实数根

B．有两个相等的实数根

C．无实数根

D．无法确定根的情况

下列方程中，没有实数根的是（ ）

A．x^2-4x+4="0"

B．x^2-2x+5=0

C．x^2-2x="0"

D．x^2-2x-3=0

一元二次方程 $x^2+4x-3=0$的两根为 $x_1$， $x_2$ ，则 $x_1-x_2$的值是（ ）

A．

$4$

B．

$-4$

C．

$3$

D．

$-3$

一元二次方程x²﹣2x+1=0的根的情况为（ ）

A．有两个相等的实数根	B．有两个不相等的实数根
C．只有一个实数根	D．没有实数根

用配方法解一元二次方程x²﹣6x﹣4=0，下列变形正确的是（   ）

A．（x﹣6）^2=﹣4+36

B．（x﹣6）^2=4+36

C．（x﹣3）^2=﹣4+9

D．（x﹣3）^2=4+9

在一次学习交流会上，每两名学生握手一次，经统计共握手253次．若设参加此会的学生为名，根据题意可列方程为 （      ）

A．	B．
C．	D．