已知关于x的方程x2+(m+2)x+2m﹣1=0.
(1)求证:方程有两个不相等的实数根.
(2)若1是该方程的一个根.求m的值并求出此时方程的另一个根.
某商场销售一批名牌衬衫,平均每天可售出20件,每件赢利40元,为了扩大销售,增加利润,尽量减少库存,商场决定采取适当的降价措施.经调查发现,如果每件衬衫每降价1元,商场平均每天可多售出2件;
(1)若商场平均每天要赢利1200元,每件衬衫应降价多少元?
(2)每件衬衫降价多少元时,商场平均每天赢利最多?
定义符号 的含义为:当
的含义为:当 时,
时, 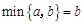 ;当
;当 时,
时,  .如:
.如: ,
, .
.
(1)求 ;
;
(2)已知 , 求实数
, 求实数 的取值范围;
的取值范围;
(3)当 时,
时, .直接写出实数
.直接写出实数 的取值范围.
的取值范围.
“创卫工作人人参与,环境卫生人人受益”,我区创卫工作已进入攻坚阶段.某校拟整修学校食堂,现需购买A、B两种型号的防滑地砖共60块,已知A型号地砖每块80元,B型号地砖每块40元.
(1)若采购地砖的费用不超过3200元,那么,最多能购买A型号地砖多少块?
(2)某地砖供应商为了支持创卫工作,现将A、B两种型号的地砖单价都降低a%,这样,该校花费了2560元就购得所需地砖,其中A型号地砖a块,求a的值.
已知关于x的一元二次方程x2+2(k﹣1)x+k2﹣1=0有两个不相等的实数根.
(1)求实数k的取值范围;
(2)0可能是方程的一个根吗?若是,请求出它的另一个根;若不是,请说明理由.
某花圃用花盆培育某种花苗,原来每盆植入3株花苗时,平均每株可盈利3元.经过试验发现若每盆多植入1株花苗,则平均每株盈利就减少0.5元.为使每盆培育花苗的盈利达到10元,则每盆应该植入花苗多少株?
某种品牌服装平均每天销售20件,每件盈利44元.销售过程中发现,在每件降价不超过10元的情况下,若每件降价1元,每天可多售5件.
(1)若每件降价2元,则每天售出 件,共盈利 元;
(2)如果销售这种品牌的服装每天要盈利2380元,求每件应降价多少元.
用配方法解一元二次方程 .请结合题意填空,完成本题的解答.
.请结合题意填空,完成本题的解答.
解:方程变形为 ,.......................第一步
,.......................第一步
配方,得 ........................................第二步
........................................第二步
移项,得 ...........................................第三步
...........................................第三步
两边开平方,得 ....................................第四步
....................................第四步
即 或
或 .................................第五步
.................................第五步
所以 ,
, ...................................第六步
...................................第六步
(1)上述解法错在第 步;
(2)请你用配方法求出该方程的解.
试题篮
()