初中数学二次函数在给定区间上的最值试题

二次函数的图象与x轴的交点坐标为      

已知二次函数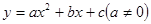的图象如图所示，有下列5个结论：
①＞0；②b＜a+c；③a+b+c＞0；④2a-b＞0；⑤9a-3b+c＜0其中正确的有

A．2个

B．3个

C．4个

D．5个

抛物线的顶点坐标是（     ）

A．(1,3)

B．(-1,3)

C．(-1,-3)

D．(-2,3)

已知＜0，二次函数的图象上有三个点A（－2，），B（1，），C（3，），则有（     ）

A．＜＜

B．＜＜

C．＜＜

D．＜＜

抛物线的顶点坐标是（     ）

A．（0，0）

B．（0，3）

C．（－2，3）

D．（3，－2）

已知抛物线y＝－x²＋mx－m＋2．  
（Ⅰ）若抛物线与x轴的两个交点A、B分别在原点的两侧，并且AB＝，试求m的值；
（Ⅱ）设C为抛物线与y轴的交点，若抛物线上存在关于原点对称的两点M、N，并且 △MNC的面积等于27，试求m的值

（本题8分）
如图，已知抛物线与直线y=x交于A、B两点，与y轴交于点C，OA＝OB，BC∥x轴

(1)求抛物线的解析式．
(2)设D、E是线段AB上异于A、B的两个动点(点E在点D的上方)，DE＝，过D、E两点分别作y轴的平行线，交抛物线于F、G，若设D点的横坐标为x，四边形DEGF的面积为y，求x与y之间的关系式，写出自变量x的取值范围，并回答x为何值时，y有最大值．

抛物线的顶点坐标为（   ，  ）

请选择一组你喜欢的的值，使二次函数的图象同时满足下列条件：①开口向下，②当时，随的增大而增大；当时，随的增大而减小．这样的二次函数的解析式可以是          

平移抛物线，使它经过原点，写出平移后抛物线的一个解析式_______

小敏在今年的校运动会跳远比赛中跳出了满意一跳，函数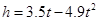（t的单位：s，h的单位：m）可以描述他跳跃时重心高度的变化，则他起跳后到重心最高时所用的时间是（　　　）

A．0．71s

B．0．70s

C．0．63s

D．0．36s

抛物线的对称轴是 (    )

A．x＝-2

B．x＝4

C．x＝2

D．x＝-4

如图，在平面直角坐标系中，抛物线向左平移1个单位，再向下平移4个单位，得到抛物线.所得抛物线与轴交于两点（点在点的左边），与轴交于点，顶点为.

（1）求的值；
（2）判断的形状，并说明理由；
（3）在线段上是否存在点，使与相似.若存在，求出点的坐标；若不存在，说明理由

如图，已知抛物线经过，两点，顶点为．

（1）求抛物线的解析式；
（2）将绕点顺时针旋转90°后，点落到点的位置，  
将抛物线沿轴平移后经过点，求平移后所得图象的函数关系式；（3）设（2）中平移后，所得抛物线与轴的交点为，顶点为，若点在平移后的抛物线上，且满足的面积是面积的2倍，求点的坐标．

一快餐店试销某种套餐，试销一段时间后发现，每份套餐的成本为5元，该店每天固定支出费用为600元(不含套餐成本)．若每份售价不超过10元，每天可销售400份；若每份售价超过10元，每提高1元，每天的销售量就减少40份．为了便于结算，每份套餐的售价x(元)取整数，用y(元)表示该店日净收入．(日净收入＝每天的销售额－套餐成本－每天固定支出)
(1)求y与x的函数关系式；
(2)若每份套餐售价不超过10元，要使该店日净收入不少于800元，那么每份售价最少不低于多少元？
(3)该店既要吸引顾客，使每天销售量较大，又要有较高的日净收入．按此要求，每份套餐的售价应定为多少元？此时日净收入为多少？