下面每个图是由若干个圆点组成的形如四边形的图案,当每条边(包括顶点)上有n(n≥2)个圆点时,图案的圆点数为Sn,按此规律推算Sn 关于n的关系式为:__________________.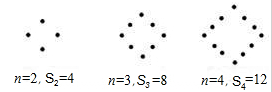
平面直角坐标系中,O为坐标原点,点A的坐标为(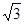 ,1),将OA绕原点按逆时针方向旋转30°得OB,则点B的坐标为【 】
,1),将OA绕原点按逆时针方向旋转30°得OB,则点B的坐标为【 】
A.(1,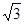 ) ) |
B.( -1,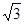 ) ) |
C.(0,2) | D.(2,0) |
阅读下列材料:
在学习小组,小明接到这样一个任务:把一个正方形分割成9个、10个和11个小正方形。为完成任务,小明先学习了两种简单的“基本分割法”。
基本分割法1:如图①,把一个正方形分割成4个小正方形,即在原来1个正方形的基础上增加了3个正方形.
基本分割法2:如图②,把一个正方形分割成6个小正方形,即在原来1个正方形的基础上增加了5个正方形.
学习了上述两种“基本分割法”后,小明很从容地就完成了分割的任务:
(1)把一个正方形分割成9个小正方形.
方法一:如图③,把图①中的任意1个小正方形按“基本分割法2”进行分割,就可增加5个小正方形,从而分割成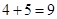 (个)小正方形.
(个)小正方形.
方法二:如图④,把图②中的任意1个小正方形按“基本分割法1”进行分割,就可增加3个小正方形,从而分割成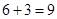 (个)小正方形.
(个)小正方形.
(2)把一个正方形分割成10个小正方形.
如图⑤,把图①中的任意2个小正方形按“基本分割法1”进行分割,就可增加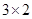 个小正方形,从而分割成
个小正方形,从而分割成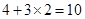 (个)小正方形.
(个)小正方形.
请你参照上述分割方法解决下列问题(只要求画图,不用说明分割方法):
(1)请你替小明同学把图⑥给出的正方形分割成11个小正方形;
(2)仿照基本分割法1:请把图a中的正三角形分割成4个小正三角形;
(3)仿照基本分割法2:请把图b 中的正三角形分割成6个小正三角形;
(4)分别把图c和图d中的正三角形分割成9个和10个小正三角形.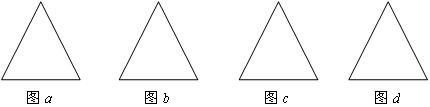
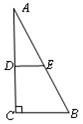
如图,在一张△ABC纸片中, ∠C=90°, ∠B=60°,DE是中位线,现把纸片沿中位线DE剪开,计划拼出以下四个图形:①邻边不等的矩形;②等腰梯形;③有一个角为锐角的菱形;④正方形.那么以上图形一定能被拼成的个数为( )
| A.1 | B.2 | C.3 | D.4 |
如图  将如何变换才能够将下图所缺位置填满,形成两层阴影( )
将如何变换才能够将下图所缺位置填满,形成两层阴影( )
| A.顺时针旋转180度再向下平移 | B.逆时针旋转180度再向下平移 |
| C.顺时针旋转90度再向下平移 | D.逆时针旋转90度再向下平移 |

如图,自行车每节链条的长度为2.5cm,交叉重叠部分的圆的直径为0.8cm.
(1)4节链条长 cm;
(2)n节链条长 cm;
(3)如果一辆22型自行车的链条由50节这样的链条组成,那么这辆自行车上的链条总长度是多少?
如图,边长为 的正方形纸片剪出一个边长为m的正方形之后,剩余部分可剪拼成一个矩形,若拼成的矩形一边长为4,则另一边长为
的正方形纸片剪出一个边长为m的正方形之后,剩余部分可剪拼成一个矩形,若拼成的矩形一边长为4,则另一边长为 
如图,连接在一起的两个正方形的边长都为1cm,一个微型机器人由点A开始按ABCDEFCGA…的顺序沿正方形的边循环移动.①第一次到达G点时移动了 ▲ cm;②当微型机器人移动了2012cm时,它停在 ▲ 点.
现有一张长和宽之比为2:1的长方形纸片.将它折两次(第一次折后也可以打开铺平再折第二次).使得折痕将纸片分为面积相等且不重叠的四个部分(称为一个操作),如图甲(虚线表示折痕).
除图甲外,请你再给出三个不同的操作,分别将折痕画在图①至图③中(规定:一个操作得到的四个图形,和另一个操作得到的四个图形,如果能够“配对”得到四组全等的图形,那么就认为是相同的操作.如图乙和图甲是相同的操作).
图① 图② 图③
(本题8分)老师说:“今天我来表演一个数学魔术。”说完便在黑板上画出下面两个图:
⑴请你借助数学知识对这两个图通过计算验证说明拼接是否可行,若不行请说明理由;
⑵画出正确的拼接图(单位
 ),并作简单说明.
),并作简单说明.
如图所示,在4×4的菱形斜网格图中(每一个小菱形的边长为1,有一个角是60°),菱形ABCD的边长为2,E是AD的中点,按CE将菱形ABCD剪成①、②两部分,用这两部分可以分别拼成直角三角形、等腰梯形、矩形,要求所拼成图形的顶点均落在格点上.
(1)在下面的菱形斜网格中画出示意图;
 |
|
|
(2)判断所拼成的三种图形的面积( )、周长(
)、周长( )的大小关系(用“=”、“>”或“<”连接):
)的大小关系(用“=”、“>”或“<”连接):
如图所示, 在正方形网格中,若点
在正方形网格中,若点 的坐标为
的坐标为 ,按要求回答下列问题:
,按要求回答下列问题:
在图中建立正确的平面直角坐标系;
根据所建立的坐标系,写出点
 和点
和点 的坐标;
的坐标;作出
 关于
关于 轴的对称图形
轴的对称图形 .(不用写作法)
.(不用写作法)
如图,“回”字形的道路宽为1米,整个“回”字形的长为8米,宽为7米,—个人从入口点A沿着道路中央走到终点B,他共走了( ).
| A.5 5米 | B.5 5.5米 | C.5 6米 | D.5 6.5米 |

一副直角三角板叠放如图所示,现将含45°角的三角板ADE固定不动,把含30°角的三角板ABC绕顶点A顺时针旋转∠α(α=∠BAD且0°<α<180°),使两块三角板至少有一组边平行。
(1)如图①,α=______°时,BC∥DE;
(2)请你分别在图②、图③的指定框内,各画一种符合要求的图形,标出α,并完成各项填空:
图②中α=______°时,______∥______;图③中α=______°时,______∥______。

试题篮
()