数学课上,张老师出示了问题:如图1,△ABC是等边三角形,点D是边BC的中点. ,且DE交△ABC外角
,且DE交△ABC外角 的平分线CE于点E,求证:AD=DE.
的平分线CE于点E,求证:AD=DE.
经过思考,小明展示了一种正确的解题思路:取AB的中点M,连接MD,则△BMD是等边三角形,易证△AMD≌△DCE,所以AD=DE.在此基础上,同学们作了进一步的研究:
(1)小颖提出:如图2,如果把“点D是边BC的中点”改为“点D是边BC上(除B,C外)的任意一点”,其它条件不变,那么结论“AD=DE”仍然成立,你认为小颖的观点正确吗?如果正确,写出证明过程;如果不正确,请说明理由;
(2)小亮提出:如图3,点D是BC的延长线上(除C点外)的任意一点,其他条件不变,结论“AD=DE”仍然成立.你认为小华的观点 (填“正确”或“不正确”).
如图,在直角 中,∠C=90°,DC = 2,∠CAB的平分线AD交BC于点D,DE垂直平分AB.求∠B的度数和DB的长.
中,∠C=90°,DC = 2,∠CAB的平分线AD交BC于点D,DE垂直平分AB.求∠B的度数和DB的长.
如图,△ABD ≌△EBD, △DBE ≌△DCE, B, E, C在一条直线上.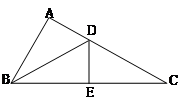
BD是∠ABE的平分线吗?为什么
DE⊥BC,BE=EC吗?为什么
如图10,有一湖的湖岸在A、B之间呈一段圆弧状,A、B间的距离 不能直接测得.你能用已学过的知识或方法设计测量方案,求出A、B间的距离吗?
不能直接测得.你能用已学过的知识或方法设计测量方案,求出A、B间的距离吗?
如图,在三角形ABC中,AB=AC=13,AD、BE是高,AD=12。
(1)求BC的长;(3分。)
(2)求DE的长;(2分。)
(3)求BE的长。(2分。)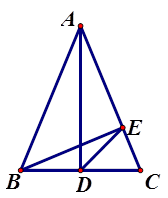
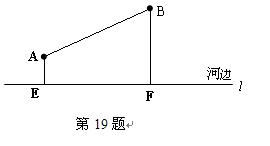
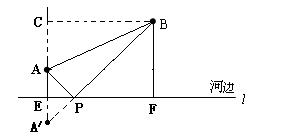
如图,要在河边修建一个水泵站,分别向张村A和李庄B送水,已知张村A、李庄B到河边的距离分别为2km和7km,且张、李二村庄相距13km.
(1). 水泵应建在什么地方,可使所用的水管最短?请在图中设计出水泵站的位置;
(2). 如果铺设水管的工程费用为每千米1500元,为使铺设水管费用最节省,请求出最节省的铺设水管的费用为多少元?
如图,等边△ABC中,AO是∠BAC的角平分线,D为AO上一点,以CD为一边且在CD下方作等边△CDE,连接BE.
(1)求证:△ACD≌△BCE;
(2)延长BE至Q,P为BQ上一点,连接CP、CQ使CP=CQ=5,若BC=8时,求PQ的长.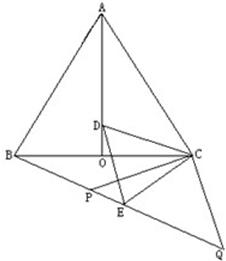
试题篮
()