如图,已知⊙O是△ABC的外接圆,AC是直径,∠A=30°,BC=2,点D是AB的中点,连接DO并延长交⊙O于点P,过点P作PF⊥AC于点F.
(1)求劣弧PC的长;(结果保留π)
(2)求阴影部分的面积.(结果保留π).
每位同学都能感受到日出时美丽的景色.右图是一位同学从照片上剪切下来的画面,“图上”太阳与海平线交于A﹑B两点,他测得“图上”圆的半径为5厘米,AB=8厘米,若从目前太阳所处位置到太阳完全跳出海面的时间为16分钟,求“图上”太阳升起的速度.
由“不在同一直线上的三点确定一个圆”,可以判断平面直角坐标系内的三个点A(3,0)、B(0,﹣4)、C(2,﹣3) 确定一个圆(填“能”或“不能”).
(12分) 已知⊙O的半径为2,∠AOB=120°。
(1)点O到弦AB的距离为 .
(2)若点P为优弧AB上一动点(点P不与A、B重合),设∠ABP=α,将△ABP沿BP折叠,得到A点的对称点为A';
①若∠α=30°,试判断点A'与⊙O的位置关系;
②若BA'与⊙O相切于B点,求BP的长;
③若线段BA'与优弧APB只有一个公共点,直接写出α的取值范围.

(本题12分).如图1,在平面直角坐标系xoy中,M是x轴正半轴上一点,⊙M与x轴的正半轴交于A,B两点,A在B的左侧,且OA,OB的长是方程x2-12x+27=0的两根,ON是⊙M的切线,N为切点,N在第四象限.
(1)求⊙M的直径的长.
(2)如图2,将△ONM沿ON翻转180°至△ONG,求证△OMG是等边三角形.
(3)求直线ON的解析式.
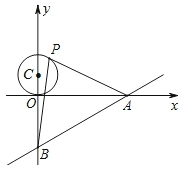
如图,已知直线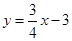 与x轴、y轴分别交于A、B两点,P是以C(0,1)为圆心,1为半径的圆上一动点,连结PA、PB.则△PAB面积的最大值是( )
与x轴、y轴分别交于A、B两点,P是以C(0,1)为圆心,1为半径的圆上一动点,连结PA、PB.则△PAB面积的最大值是( )
A.8 B.12 C.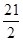 D.
D.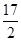
有一半圆片(其中圆心角∠AED=52°)在平面直角坐标系中,按如图所示放置,若点A可以沿y轴正半轴上下滑动,同时点B相应地在x轴上正半轴上滑动,当∠OAB=n°时,半圆片上的点D与原点O距离最大,则n为( )

| A.64 | B.52 | C.38 | D.26 |
如图,已知△ABC,外心为O,BC=6,∠BAC=60°,分别以AB、AC为腰向形外作等腰直角三角形△ABD与△ACE,连接BE、CD交于点P,则OP的最小值是_________.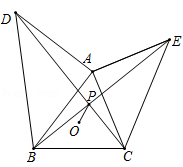
如图,在平面直角坐标系中,一段圆弧经过格点A、B、C.
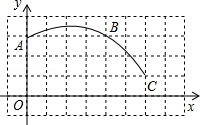
(1)请写出该圆弧所在圆的圆心O的坐标 ;
(2)⊙O的半径为 (结果保留根号);
(3)求 的长(结果保留π).
的长(结果保留π).
已知⊙O的直径为10,点A,点B,点C在⊙O上,∠CAB的平分线交⊙O于点D.
(Ⅰ)如图①,若BC为⊙O的直径,AB=6,求AC,BD,CD的长;
(Ⅱ)如图②,若∠CAB=60°,求BD的长.
如图,在平面直角坐标系中,矩形ABCO的面积为15,边OA比OC大2.E为BC的中点,以OE为直径的⊙O′交x轴于D点,过点D作DF⊥AE于点F.
(1)求OA、OC的长;
(2)求证:DF为⊙O′的切线;
(3)由已知可得,△AOE是等腰三角形.那么直线BC上存不存在除点E以外的点P,使△AOP也是等腰三角形?如果不存在,说明理由;如果存在,直接写出P点的坐标.
如图,AB为⊙O的直径,D、T是圆上的两点,且AT平分∠BAD,过点T作AD的延长线的垂线PQ,垂足为C.

(1)求证:PQ是⊙O的切线;
(2)已知⊙O的半径为2,若过点O作OE⊥AD,垂足为E,OE=  ,求弦AD的长.
,求弦AD的长.
(本题9分)如图, 点
点 在
在 轴的正半轴上,
轴的正半轴上, ,
, ,
, .点
.点 从点
从点 出发,沿
出发,沿 轴向左以每秒1个单位长的速度运动,运动时间为
轴向左以每秒1个单位长的速度运动,运动时间为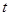 秒.
秒.

(1)点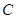 的坐标是 ;
的坐标是 ;
(2)当 时,求
时,求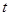 的值;
的值;
(3)以点 为圆心,
为圆心, 为半径的
为半径的 随点
随点 的运动而变化,当
的运动而变化,当 与四边形
与四边形 的边(或边所在的直线)相切时,求
的边(或边所在的直线)相切时,求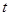 的值.
的值.
(本题6分)如图,四边形OABC是平行四边形,以O为圆心,OA为半径的圆交AB于D,延长AO交⊙O于E,连接CD,CE,若CE是⊙O的切线,解答下列问题:
(1)求证:CD是⊙O的切线;
(2)若平行四边形OABC的两边长是方程 的两根,求平行四边形OABC的面积.
的两根,求平行四边形OABC的面积.
问题提出:如图1,在Rt△ABC中,∠ACB=90°,CB=4,CA=6,⊙C半径为2,P为圆上一动点,连结AP,BP,求AP+ BP的最小值.
BP的最小值.

尝试解决:为了解决这个问题,下面给出一种解题思路:如图2,连接CP,在CB上取点D,使CD=1,则有 =
= ,又∵∠PCD=∠BCP,∴△PCD∽△BCP,∴
,又∵∠PCD=∠BCP,∴△PCD∽△BCP,∴ =
= ,∴PD=
,∴PD= BP,∴AP+
BP,∴AP+ BP=AP+PD.
BP=AP+PD.
请你完成余下的思考,并直接写出答案:AP+ BP的最小值为 .
BP的最小值为 .
自主探索:在“问题提出”的条件不变的情况下,  AP+BP的最小值为 .
AP+BP的最小值为 .
拓展延伸:已知扇形COD中,∠COD=90º,OC=6,OA=3,OB=5,点P是 上一点,求2PA+PB的最小值.
上一点,求2PA+PB的最小值.
试题篮
()