如图,△ABC中,AB=AC,以AB为直径作⊙O,交BC于点D,交CA的延长线于点E,连接AD、DE.
(1)求证:D是BC的中点;
(2)若DE=3,BD—AD=2,求⊙O的半径;
(3)在(2)的条件下,求弦AE的长.
图1、图2为同一长方体房间的示意图,图3为该长方体的表面展开图.
(1)蜘蛛在顶点A′处.
①苍蝇在顶点B处时,试在图1中画出蜘蛛为捉住苍蝇,沿墙面爬行的最近路线;
②苍蝇在顶点C处时,图2中画出了蜘蛛捉住苍蝇的两条路线,往天花板ABCD爬行的最近路线A′GC和往墙面BB′C′C爬行的最近路线A′HC,试通过计算判断哪条路线更近;
(2)在图3中,半径为10dm的⊙M与D′C′相切,圆心M到边CC′的距离为15dm,蜘蛛P在线段AB上,苍蝇Q在⊙M的圆周上,线段PQ为蜘蛛爬行路线,若PQ与⊙M相切,试求PQ长度的范围.
如图,在矩形
中,点
在边
上,且
,过点
作
,垂足为点
.

(1)求证:
;
(2)以
为圆心,
为半径作圆弧交
于点
.若
,试求
的长.
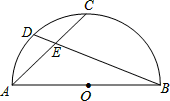
如图,AB是半圆O的直径,点C是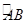 的中点,点D是
的中点,点D是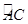 的中点,连接AC.BD交于点E,则
的中点,连接AC.BD交于点E,则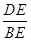 =( )
=( )
A.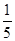 B.
B.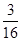 C.
C.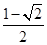 D.
D.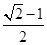
在正方形ABCD中,AD=2,l是过AD中点P的一条直线.O是l上一点,以O为圆心的圆经过点A、D,直线l与⊙O交于点E、F(E、F不与A、D重合,E在F的上面).
(1)如图,若点F在BC上,求证:BC与⊙O相切.并求出此时⊙O的半径.
(2)若⊙O半径为 ,请直接写出∠AED的度数.
,请直接写出∠AED的度数.
如图,OA.OB是⊙O的半径且OA⊥OB,作OA的垂直平分线交⊙O于点C.D,连接CB.AB.
求证:∠ABC=2∠CBO.
如图,点D是等边△ABC中BC边的延长线上一点,且AC=CD,以AB为直径作⊙O,分别交边AC、BC于点E、点F
(1)求证:AD是⊙O的切线;
(2)连接OC,交⊙O于点G,若AB=4,求线段CE、CG与 围成的阴影部分的面积S.
围成的阴影部分的面积S.
如图,点C是半圆O的半径OB上的动点,作PC⊥AB于C.点D是半圆上位于PC左侧的点,连接BD交线段PC于E,且PD=PE.
(1)求证:PD是⊙O的切线;
(2)若⊙O的半径为4 ,PC=8
,PC=8 ,设OC=x,PD2=y.
,设OC=x,PD2=y.
①求y关于x的函数关系式;
②当x= 时,求tanB的值.
时,求tanB的值.
圆锥的侧面展开图是一个弧长为12π的扇形,则这个圆锥底面积的半径是( )
| A.24 | B.12 | C.6 | D.3 |
如图,直线 与坐标轴交于AB两点,点
与坐标轴交于AB两点,点 是
是 轴上一动点,以点M为圆心,2个单位长度为半径作⊙M,当⊙M与直线
轴上一动点,以点M为圆心,2个单位长度为半径作⊙M,当⊙M与直线 想切时,
想切时, 的值为__________________.
的值为__________________.
如图,在△ABC中,AB=AC,以AC为直径作⊙O交BC于点D,过点D作⊙O的切线,交AB于点E,交CA的延长线于点F.
(1)求证:FE⊥AB;
(2)当EF=6, 时,求DE的长.
时,求DE的长.
在底面直径为2cm,高为3cm的圆柱体侧面上,用一条无弹性的丝带从A至C按如图所示的圈数缠绕,则丝带的最短长度为 cm.(结果保留π)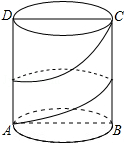
如图,在△ABC中,∠C=90°,AC+BC=8,点O是斜边AB上一点,以O为圆心的⊙O分别与AC,BC相切于点D,E.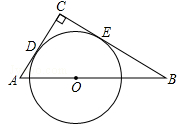
(1)当AC=2时,求⊙O的半径;
(2)设AC=x,⊙O的半径为y,求y与x的函数关系式.
如图,直线 ⊥线段
⊥线段 于点
于点 ,点
,点 在
在 上,且
上,且 ,点
,点 是直线
是直线 上的动点,作点
上的动点,作点 关于直线
关于直线 的对称点
的对称点 ,直线
,直线 与直线
与直线 相交于点
相交于点 ,连接
,连接
(1)如图1,若点 与点
与点 重合,则∠
重合,则∠ = °,线段
= °,线段 与
与 的比值为 ;
的比值为 ;
(2)如图2,若点 与点
与点 不重合,设过
不重合,设过 、
、 、
、 三点的圆与直线
三点的圆与直线 相交于
相交于 ,连接
,连接 。求证:①
。求证:① =
= ;②
;② =2
=2 ;
;
(3)如图3, ,
, ,则满足条件
,则满足条件 的点都在一个确定的圆上,在以下两小题中选做一题:
的点都在一个确定的圆上,在以下两小题中选做一题:
①如果你能发现这个确定圆的圆心和半径,那么不必写出发现过程,只要证明这个圆上的任意一点Q,都满足QA=2QB
②如果你不能发现这个确定圆的圆心和半径,那么请取几个特殊位置的 点,如点
点,如点 在直线
在直线 上、点
上、点 与点
与点 重合等进行探究,求这个圆的半径
重合等进行探究,求这个圆的半径
已知⊙O是以AB为直径的△ABC的外接圆,OD∥BC交⊙O于点D,交AC于点E,连接AD、BD,BD交AC于点F.
(1)求证:BD平分∠ABC;
(2)延长AC到点P,使PF=PB,求证:PB是⊙O的切线;
(3)如果AB=10,cos∠ABC= ,求AD.
,求AD.
试题篮
()