初中数学圆幂定理解答题

（本题满分10分，第（1）小题满分4分，第（2）小题满分6分）如图5，点C、D分别在扇形AOB的半径OA、OB的延长线上，且OA＝3，AC＝2，CD平行于AB，并与弧AB相交于点M、N．
（1）求线段OD的长；
（2）若，求弦MN的长．

如图，在△ABC，AB=AC，以AB为直径的⊙O分别交AC、BC于点D、E，点F在AC的延长线上，且∠CBF=∠CAB．
（1）求证：直线BF是⊙O的切线；
（2）若AB=5，sin∠CBF=，求BC和BF的长．

如图，射线PG平分∠EPF，O为射线PG上一点，以O为圆心，10为半径作⊙O，分别与∠EPF的两边相交于A、B和C、D，连接OA，此时有OA∥PE．
（1）求证：AP=AO；
（2）若tan∠OPB=，求弦AB的长；
（3）若以图中已标明的点（即P、A、B、C、D、O）构造四边形，则能构成菱形的四个点为_________，能构成等腰梯形的四个点为__________或__________或___________

如图6，AB是⊙O的直径，BC⊥AB于点B，连接OC交⊙O于   
点E，弦AD∥OC．
(1)求证：      ；
(2)求证：CD是⊙O的切线．

 

 
（图6）

如图，在Rt△ABC中，∠B＝90°，AB＝1，BC＝，以点C
为圆心，CB为半径的弧交CA于点D；以点A为圆心，AD为半径的弧交AB于点E．
（1）求AE的长度；
（2）分别以点A、E为圆心，AB长为半径画弧，两弧交于点F（F与C在AB两侧），连接AF、EF，设EF交弧DE所在的圆于点G，连接AG，试猜想∠EAG的大小，并说明理由．

 

如图，在平面直角坐标系中，O为坐标原点，P是反比例函数
y＝（x＞0）图象上的任意一点，以P为圆心，PO为半径的圆与x、y轴分别交于点A、
B．
（1）判断P是否在线段AB上，并说明理由；
（2）求△AOB的面积；
（3）Q是反比例函数y＝（x＞0）图象上异于点P的另一点，请以Q为圆心，QO
半径画圆与x、y轴分别交于点M、N，连接AN、MB．求证：AN∥MB．

 

如图，在锐角△ABC中，AC是最短边；以AC中点O为圆心，AC长为半径作⊙O，交BC于E，过O作OD∥BC交⊙O于D，连结AE、AD、DC．
（1）求证：D是 弧AE 的中点；
（2）求证：∠DAO =∠B+∠BAD；
（3）若 ，且AC=4，求CF的长.

 

在圆内接四边形ABCD中，CD为∠BCA外角的平分线，F为弧AD上一点，
BC=AF，延长DF与BA的延长线交于E．
⑴求证△ABD为等腰三角形．
⑵求证AC•AF=DF•FE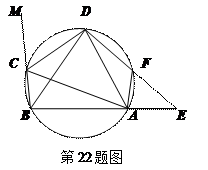

．如图，点A、B在⊙O上，直线AC是⊙O的切线，OD⊥OB，连接AB交OC于点D．
⑴求证：AC=CD
⑵若AC=2，AO=，求OD的长度．

如图所示，AC为⊙O的直径且PA⊥AC，BC是⊙O的一条弦，直线PB交直线AC于点D，．
（1）求证：直线PB是⊙O的切线；
（2）求cos∠BCA的值．

（本小题满分5分）已知：如图，在中，，点在上，以为圆心，长为半径的圆与分别交于点，且．
（1）判断直线与的位置关系，并证明你的结论；
（2）若，=，求的值．

如图，⊙O的直径AB为10cm，弦AC为6cm，∠ACB的平分线交⊙O于D，求BC，AD，BD的长．