初中数学立体图形试题

如图，圆锥的底面半径高则这个圆锥的侧面积是（   ）

A．

B．

C．

D．

回答下列问题：
⑴如图所示的甲、乙两个平面图形能折什么几何体？

（2）由多个平面围成的几何体叫做多面体.若一个多面体的面数为，顶点个数为，棱数为，分别计算第（1）题中两个多面体的的值？你发现什么规律？
（3）应用上述规律解决问题：一个多面体的顶点数比面数大8，且有50条棱，求这个几何体的面数.

用若干个相同的小立方块搭建一个几何体，使从它的正面和上面看到的图形如图所示，动手搭一搭，你的搭法唯一吗？
（1）最多需要多少个小立方块？画出从左面看该几何体得到的图形；
（2）最少需要多少个小立方块？画出从左面看该几何体得到的图形。

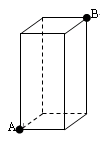
如图所示，有一个长、宽各2米，高为3米且封闭的长方体纸盒，一只昆虫从顶点A要爬到顶点B，那么这只昆虫爬行的最短路程为

A．3米

B．4米

C．5米

D．6米

用一个边长为10cm的正方形围成一个圆柱的侧面（接缝略去不计），求该圆柱的体积.

如下图,是边长为1 m的正方体，有一蜘蛛潜伏在A处，B处有一小虫被蜘蛛网粘住，请利用平面图形，画出蜘蛛爬行的最短路线.

薄薄的硬币在桌面上转动时，看上去象球，这说明了____  _____________.

如果长方体从一点出发的三条棱长分别为2、3、4，则该长方体的表面积为__    __

用一个宽2cm，长3cm的矩形卷成一个圆柱，则此圆柱的侧面积为_______________.

下列四个图中，是三棱锥的表面展开图的是 （  ）

下列图形不是立体图形的是 （  ）                                      

A．球

B．圆柱

C．圆锥

D．圆

若干个正方体形状的积木摆成如图所示的塔形，平放于桌面上，上面正方体的下底四个顶点是下面相邻正方体的上底各边中点，最下面的正方体棱长为1，如果塔形露在外面的面积超过7，则正方体的个数至少是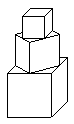

A．2

B．3

C．4

D．5

如图，上下底面为全等的正六边形礼盒，其正视图与侧视图均由矩形构成，正视图中大矩形边长如图所示，侧视图中包含两全等的矩形，如果用彩色胶带如图包扎礼盒，所需胶带长度至少为（   ）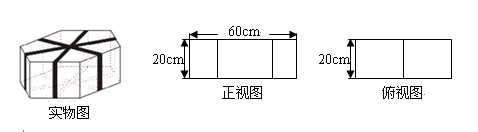

A．320cm

B．395.24 cm

C．431.76 cm

D．480 cm

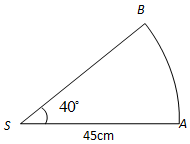
如图，扇形彩色纸的半径为45cm，圆心角为，用它制作一个圆锥形火炬模型的侧面（接头忽略不计），则这个圆锥的高约为         cm．（结果精确到0.1cm．参考数据：，，，）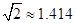

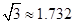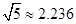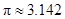如图（1）所示为一上面无盖的正方体纸盒，现将其剪开展成平面图，如图（2）所示．已知展开图中每个正方形的边长为1．
（1）求在该展开图中可画出最长线段的长度？这样的线段可画几条？
（2）试比较立体图中与平面展开图中的大小关系？