计算:
(1)-3-5+12;
(2)(-81)÷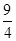 ×
× ÷(-16);
÷(-16);
(3)-32-25×(-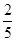 )2;
)2;
(4)-24×(-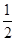 +
+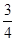 -
-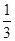 );
);
(5)-14-(1+0.5)×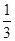 ÷4;
÷4;
(6)-22×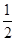 -(-1
-(-1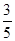 )2÷(-
)2÷(-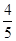 )-(-1)5.
)-(-1)5.
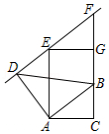
如图,在 中, , , .线段 由线段 绕点 按逆时针方向旋转 得到, 由 沿 方向平移得到,且直线 过点 .
(1)求 的大小;
(2)求 的长.
某公司开发出一款新的节能产品,该产品的成本价为6元 件,该产品在正式投放市场前通过代销点进行了为期一个月(30天)的试销售,售价为8元 件,工作人员对销售情况进行了跟踪记录,并将记录情况绘成图象,图中的折线 表示日销售量 (件)与销售时间 (天)之间的函数关系,已知线段 表示的函数关系中,时间每增加1天,日销售量减少5件.
(1)第24天的日销售量是 件,日销售利润是 元.
(2)求 与 之间的函数关系式,并写出 的取值范围;
(3)日销售利润不低于640元的天数共有多少天?试销售期间,日销售最大利润是多少元?

根据频数分布表或频数分布直方图求加权平均数时,统计中常用各组的组中值代表各组的实际数据,把各组的频数看作相应组中值的权,请你依据以上知识,解决下面的实际问题.
为了解5路公共汽车的运营情况,公交部门统计了某天5路公共汽车每个运行班次的载客量,并按载客量的多少分成 , , , 四组,得到如下统计图:
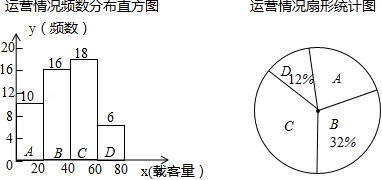
(1)求 组对应扇形圆心角的度数,并写出这天载客量的中位数所在的组;
(2)求这天5路公共汽车平均每班的载客量;
(3)如果一个月按30天计算,请估计5路公共汽车一个月的总载客量,并把结果用科学记数法表示出来.
试题篮
()