已知抛物线y=ax2+bx+c与x轴交于点A(1,0),B(3,0),且过点C(0,-3).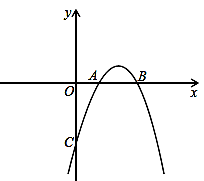
(1)求抛物线的解析式和顶点坐标;
(2)请你写出一种平移的方法,使平移后抛物线的顶点落在直线y=-x上,并写出平移后抛物线的解析式.
已知关于 的一元二次方程
的一元二次方程 的两个实数根
的两个实数根 、
、 的值分别是□ABCD的两边AB、AD的长.
的值分别是□ABCD的两边AB、AD的长.
(1)如果 ,试求□ABCD的周长;
,试求□ABCD的周长;
(2)当 为何值时,□ABCD是菱形?
为何值时,□ABCD是菱形?
如图,已知抛物线 的对称轴为直线
的对称轴为直线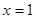 ,交
,交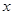 轴于
轴于 、
、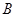 两点,交
两点,交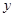 轴于
轴于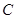 点,其中
点,其中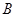 点的坐标为(3,0)。
点的坐标为(3,0)。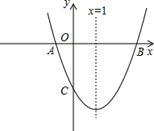
(1)直接写出 点的坐标;
点的坐标;
(2)求二次函数 的解析式。
的解析式。
如图,在RtΔABC中,∠C=90º,AC=4cm,BC=3cm.动点M、N从点C同时出发,均以每秒1cm的速度分别沿CA、CB向终点A、B移动,同时动点P从点B出发,以每秒2cm的速度沿BA向终点A移动。连接PM、PN。设移动时间为t(单位:秒,0<t<2.5).

(1)当t为何值时,以A、P、M为顶点的三角形与ΔABC相似?
(2)是否存在某一时刻t,使△PMN 的面积恰好是△ABC 面积的 ;若存在求t的值;若不存在,请说明理由.
;若存在求t的值;若不存在,请说明理由.
(1)(-8)-47+18-(-27)
(2)(-3)×(-9)-8×(-5)
(3)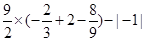
(4)计算:-5(x2-3)-2(3x2+5)
(5)化简并求值:4y2-(x2+y2)+(x2-4y2),其中x=-28,y=18
水稻种植是嘉兴的传统农业.为了比较甲、乙两种水稻的长势,农技人员从两块试验田中,分别随机抽取5棵植株,将测得的苗高数据绘制成下图: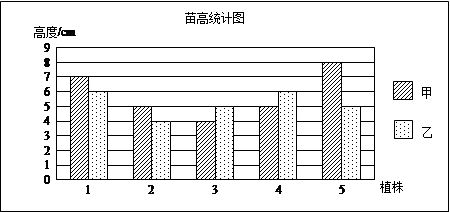
请你根据统计图所提供的数据,计算平均数和方差,并比较两种水稻的长势.
试题篮
()