初中数学解答题

如图所示，已知在直角梯形中，轴于点．动点从点出发，沿轴正方向以每秒1个单位长度的速度移动．过点作垂直于直线，垂足为．设点移动的时间为秒（），与直角梯形重叠部分的面积为．
（1）求经过三点的抛物线解析式；
（2）求与的函数关系式；
（3）将绕着点顺时针旋转，是否存在，使得的顶点或在抛物线上？若存在，直接写出的值；若不存在，请说明理由．

如图，已知抛物线经过，两点，顶点为．将绕点顺时针旋转90°后，点落到点的位置，将抛物线沿轴平移后经过点，求平移后所得图象的函数关系式；

如图，已知抛物线y=－x²+2x+3交x轴于A、B两点（点A在点B的左侧），与y轴交于点C。
（1）求点A、B、C的坐标。
（2）若点M为抛物线的顶点，连接BC、CM、BM，求△BCM的面积。
（3）连接AC，在x轴上是否存在点P使△ACP为等腰三角形，若存在，请求出点P的坐标；若不存在，请说明理由。

在云南大理坐落着美丽的大理三塔．数学活动小组开展课外实践活动，在一个阳光明媚的上午，他们去测量三塔中一塔的高度，携带的测量工具有：测角仪．皮尺．小镜子．
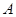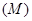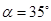（1）小华利用测角仪和皮尺测量塔高． 图1为小华测量塔高的示意图．她先在塔前的平地上选择一点，用测角仪测出看塔顶的仰角，在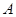点和塔之间选择一点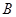，测出看塔顶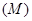的仰角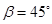，然后用皮尺量出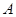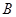．两点的距离为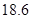m,自身的高度为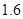m．请你利用上述数据帮助小华计算出塔的高度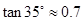（，结果保留整数）．

（2）如果你是活动小组的一员，正准备测量塔高，而此时塔影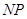的长为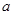m（如图2）,你能否利用这一数据设计一个测量方案？如果能，
请回答下列问题：
①在你设计的测量方案中，选用的测量工具是:；
②要计算出塔的高，你还需要测量哪些数据？．

为实现区域教育均衡发展，我市计划对某县、两类薄弱学校全部进行改造．根据预算，共需资金1575万元．改造一所类学校和两所类学校共需资金230万元；改造两所类学校和一所类学校共需资金205万元．
（1）改造一所类学校和一所类学校所需的资金分别是多少万元？
（2）若该县的类学校不超过5所，则类学校至少有多少所？
（3）我市计划今年对该县、两类学校共6所进行改造，改造资金由国家财政和地方财政共同承担．若今年国家财政拨付的改造资金不超过400万元；地方财政投入的改造资金不少于70万元，其中地方财政投入到、两类学校的改造资金分别为每所10万元和15万元．请你通过计算求出有几种改造方案？

已知：如图，在平面直角坐标系中，直线AB分别与轴交于点B、A，与反比例函数的图象分别交于点C、D，轴于点E，．
（1）求该反比例函数的解析式；
（2）求直线AB的解析式．

如图，梯形ABCD中，AD∥BC，∠BAD=90°，CE⊥AD于点E，AD=4cm，BC=2cm，AB=3cm.从初始时刻开始，动点P、Q分别从点A、B同时出发，运动速度均为1 cm/s，动点P沿A→B→C→E的方向运动，到点E停止；动点Q沿B→C→E→D的方向运动，到点D停止.设运动时间为s，PAQ的面积为y cm².（这里规定：线段是面积为0的三角形)解答下列问题：

（1）当x=" 2" s时，y=________cm²;当= s时，y=________cm²；
（2）当动点P在线段BC上运动，即3 ≤ x ≤ 5时，求y与之间的函数关系式，并求出时的值；
（3）当动点P在线段CE上运动，即5 < x ≤ 8 时，求y与之间的函数关系式；
（4）直接写出在整个运动过程中，使PQ与四边形ABCE的对角线平行的所有x的值．

如图，在平行四边形ABCD中，AD="4" cm，∠A=60°，BD⊥AD． 一动点P从A出发，以每秒1 cm的速度沿A→B→C的路线匀速运动，过点P作直线PM，使PM⊥AD ．

（1）当点P运动2秒时，设直线PM与AD相交于点E，求△APE的面积；
（2）当点P运动2秒时，另一动点Q也从A出发沿A→B→C的路线运动，且在AB上以每秒1 cm的速度匀速运动，在BC上以每秒2 cm的速度匀速运动． 过Q作直线QN，使QN∥PM． 设点Q运动的时间为t秒（0≤t≤10），直线PM与QN截平行四边形ABCD所得图形的面积为S cm²．
① 求S关于t的函数关系式；
② 求S的最大值．

如图，在等腰梯形ABCD中，AB‖CD,已知,，，以所在直线为轴，为坐标原点，建立直角坐标系，将等腰梯形ABCD绕A点按顺时针方向旋转得到等腰梯形OEFG（O、E、F、G分别是A、B、C、D旋转后的对应点）（如图）.

⑴在直线DC上是否存在一点，使为等腰三角形，若存在，写出出点的坐标，若不存在，请说明理由.
⑵将等腰梯形ABCD沿轴的正半轴平行移动，设移动后的（0<x≤6），等腰梯形ABCD与等腰梯形OEFG重叠部分的面积为，求与之间的函数关系式.并求出重叠部分的面积的最大值。

如图，梯形ABCD中，AB∥CD，∠ABC=90°，AB=8，CD=6，BC = 4，AB边上有一动点P(不与A、B重合)，连结DP，作PQ⊥DP，使得PQ交射线BC于点E，设AP=x．

⑴当x为何值时，△APD是等腰三角形？
⑵若设BE=y，求y关于x的函数关系式；
⑶若BC的长可以变化，在现在的条件下，是否存在点P，使得PQ经过点C？若存在，求出相应的AP的长；若不存在，请说明理由，并直接写出当BC的长在什么范围内时，可以存在这样的点P，使得PQ经过点C．

如图1，在直角坐标系中，O是坐标原点，点A在y轴正半轴上，二次函数y=ax²+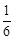x +c的图象F交x轴于B、C两点，交y轴于M点，其中B（-3，0），M（0，-1）。已知AM=BC。
（1）求二次函数的解析式；
（2）证明：在抛物线F上存在点D，使A、B、C、D四点连接而成的四边形恰好是平行四边形，并请求出直线BD的解析式；
（3）在（2）的条件下，设直线l过D且分别交直线BA、BC于不同的P、Q两点，AC、BD相交于N。
①若直线l⊥BD，如图1所示，试求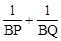的值；
②若l为满足条件的任意直线。如图2所示，①中的结论还成立吗？若成立，证明你的猜想；若不成立，请举出反例。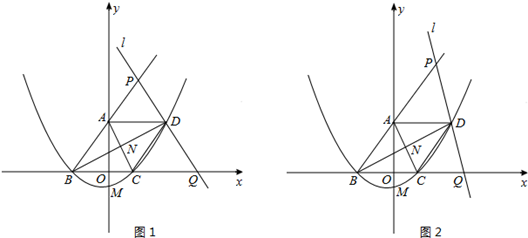

据媒体报道，近期“手足口病”可能进入发病高峰期，某校根据《学校卫生工作条例》，为预防“手足口病”，对教室进行“薰药消毒”．已知药物在燃烧机释放过程中，室内空气中每立方米含药量y（毫克）与燃烧时间x（分钟）之间的关系如图所示（即图中线段OA和双曲线在A点及其右侧的部分），根据图象所示信息，解答下列问题：
（1）写出从药物释放开始，y与x之间的函数关系式级自变量的取值范围；
（2）据测定，当空气中每立方米的含药量低于2毫克时，对人体无毒害作用，那么从消毒开始，至少在多长时间内，师生不能进入教室？

煤炭是攀枝花的主要矿产资源之一，煤炭生产企业需要对煤炭运送到用煤单位所产生的费用进行核算并纳入企业生产计划．某煤矿现有1000吨煤炭要全部运往A．B两厂，通过了解获得A．B两厂的有关信息如下表（表中运费栏“元/t•km”表示：每吨煤炭运送一千米所需的费用）：

厂别	运费（元/t•km）	路程（km）	需求量（t）
A	0.45	200	不超过600
B	a（a为常数）	150	不超过800

（2）请你运用函数有关知识，为该煤矿设计总运费最少的运送方案，并求出最少的总运费（可用含a的代数式表示）

在平面直角坐标xOy中，（如图）正方形OABC的边长为4，边OA在x轴的正半轴上，边OC在y轴的正半轴上，点D是OC的中点，BE⊥DB交x轴于点E.
⑴求经过点D、B、E的抛物线的解析式；
⑵将∠DBE绕点B旋转一定的角度后，边BE交线段OA于点F，边BD交y轴于点G，交⑴中的抛
物线于M（不与点B重合），如果点M的横坐标为，那么结论OF=DG能成立吗？请说明理由.
⑶过⑵中的点F的直线交射线CB于点P，交⑴中的抛物线在第一象限的部分于点Q，且使△PFE为等腰三角形，求Q点的坐标.

如图，在△ABC中，AB=2，AC="BC=" 5 ．
（1）以AB所在的直线为x轴，AB的垂直平分线为y轴，建立直角坐标系如图，请你分别写出A、B、C三点的坐标；
（2）求过A、B、C三点且以C为顶点的抛物线的解析式；
（3）若D为抛物线上的一动点，当D点坐标为何值时，S_△ABD=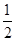S_△ABC；
（4）如果将（2）中的抛物线向右平移，且与x轴交于点A′B′，与y轴交于点C′，当平移多少个单位时，点C′同时在以A′B′为直径的圆上（解答过程如果有需要时，请参看阅读材料）．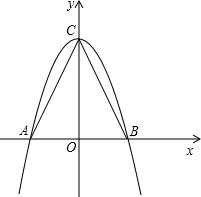

附：阅读材料
一元二次方程常用的解法有配方法、公式法和因式分解法，对于一些特殊方程可以通过换元法转化为一元二次方程求解．如解方程：y⁴-4y²+3=0．
解：令y²=x（x≥0），则原方程变为x²-4x+3=0，解得x₁=1，x₂=3．
当x₁=1时，即y²=1，∴y₁=1，y₂=-1．
当x²=3，即y²=3，∴y₃=" 3" ，y₄="-" 3 ．
所以，原方程的解是y₁=1，y₂=-1，y₃=" 3" ，y₄="-" 3 ．
再如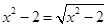，可设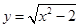，用同样的方法也可求解．