如图6,AB是⊙O的直径,BC⊥AB于点B,连接OC交⊙O于
点E,弦AD∥OC. (1)求证:;
(1)求证:;
(2)求证:CD是⊙O的切线.
 |
|||
|
|||
某县为了了解“十、一”国庆期间该县常住居民的出游情况,有关部门随机调查了1600名常住居民,并根据调查结果绘制了如下统计图:
 |
根据以上信息,解答下列各题:
(1)补全条形统计图,在扇形统计图中,直接填入出游主要目的是采集发展信息的人数的百分数;
(2)若该县常住居民共48万人,请估计该县常住居民中,利用“十、一”期间出游采集发展信息的人数;
(3)综合上述信息,用一句话谈谈你的感想.
如图5,在A岛周围25海里水域有暗礁,一轮船由西向东航行到O处时,发现A岛在北偏东
°方向,轮船继续前行20海里到达B处发现A岛在北偏东
方向,该船若不改变航向继续前进,有无触 礁的危险? (参考数据:
)
礁的危险? (参考数据:
)
在△ABC和△DEF中,∠C=∠F=90°.有如下五张背面完全相同的纸牌①、②、③、④、⑤,其正面分别写有五个不同的等式,小民将这五张纸牌背面朝上洗匀后先随机摸出一张(不放回),再随机摸出一张.请结合以上条件,解答下列问题.
(1)用树状图(或列表法)表示两次摸牌所有可能 出现的结果(纸牌用①、②、③、④、⑤表示);
出现的结果(纸牌用①、②、③、④、⑤表示);
(2)用两次摸牌的结果和∠C=∠F=90°作为条件,求能满足△ABC和△DEF全等的概率.
给出下列命题:
命题1:直线 与双曲线
与双曲线 有一个交点是(1,1);
有一个交点是(1,1);
命题2:直线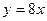 与双曲线
与双曲线 有一个交点是(
有一个交点是( ,4);
,4);
命题3:直线 与双曲线
与双曲线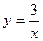 有一个交点是(
有一个交点是( ,9);
,9);
命题4:直线 与双曲线
与双曲线 有一个交点是(
有一个交点是( ,16);
,16);
……………………………………………………
(1)请你阅读、观察上面命题,猜想出命题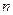 (
(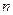 为正整数);
为正整数);
(2)请验证你猜想的命题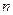 是真命题.
是真命题.
我市某建筑工地,欲拆除该工地的一危房AB(如图),准备对该危房实施定向爆破.已知距危房AB水平距离60米(BD=60米)处有一居民住宅楼,该居民住宅楼CD高15米,在该该住宅楼顶C处测得此危房屋顶A的仰角 为30°,请你通过计算说明在实施定向爆破危房AB时,该居民住宅楼有无危险?(在地面上以点B为圆心,以AB长为半径的圆形区域为危险区域,参考数据:
为30°,请你通过计算说明在实施定向爆破危房AB时,该居民住宅楼有无危险?(在地面上以点B为圆心,以AB长为半径的圆形区域为危险区域,参考数据: ,
, )
)
如图,在Rt△ABC中,∠B=90°,AB=1,BC= ,以点C
,以点C
为圆心,CB为半径的弧交CA于点D;以点A为圆心,AD为半径的弧交AB于点E.
(1)求AE的长度;
(2)分别以点A、E为圆心,AB长为半径画弧,两弧交于点F(F与C在AB两侧),连接AF、EF,设EF交弧DE所在的圆于点G,连接AG,试猜想∠EAG的大小,并说明理由.
 |
如图,在边长为2的正方形ABCD中,P为AB的中点,Q为边CD上一动点,设DQ=t(0≤t≤2),线段PQ的垂直平分线分别交边AD、BC于点M、N,过Q作QE⊥AB于点E,过M作MF⊥BC于点F.
(1)当t≠1时,求证:△PEQ≌△NFM;
(2)顺次连接P、M、Q、N,设四边形PMQN的面积为S,求出S与自变量t之间的函数关系式,并求S的最小值.
 |
如图,在平面直角坐标系中,O为坐标原点,P是反比例函数
y= (x>0)图象上的任意一点,以P为圆心,PO为半径的圆与x、y轴分别交于点A、
(x>0)图象上的任意一点,以P为圆心,PO为半径的圆与x、y轴分别交于点A、
B.
(1)判断P是否在线段AB上,并说明理由;
(2)求△AOB的面积;
(3)Q是反比例函数y= (x>0)图象上异于点P的另一点,请以Q为圆心,QO
(x>0)图象上异于点P的另一点,请以Q为圆心,QO
半径画圆与x、y轴分别交于点M、N,连接AN、MB.求证:AN∥MB.
 |
某通讯公司推出①、②两种通讯收费方式供用户选择,其中一 种有月租费,另一种无月租费,且两种收费方式的通讯时间x(分钟)与收费y(元)之间
种有月租费,另一种无月租费,且两种收费方式的通讯时间x(分钟)与收费y(元)之间
的函数关系如图所示.
(1)有月租费的收费方式是(填①或②),
月租费是元;
(2)分别求出①、②两种收费方式中y与自
变量x之间的函数关系式;
(3)请你根据用户通讯时间的多少,给出
经济实惠的选择建议.
在一个不透明的布袋中装有相同的三个小球,其上面分别标注
数字1、2、3、,现从中任意摸出一个小球,将其上面的数字作为点M的横坐标;将球放回
袋中搅匀,再从中任意摸出一个小球,将其上面的数字作为点M的纵坐标.
(1)写出点M坐标的所有可能的结果;
(2)求点M在直线y=x上的概率;
(3)求点M的横坐标与纵坐标之和是偶数的概率.
如图,为了测量某建筑物CD的高度,先在地面上用测角仪自
A处测得建筑物顶部的仰角是30°,然后在水平地面上向建筑物前进了100m,此时自B处
测得建筑物顶部的仰角是45°.已知测角仪的高度是1.5m,请你计算出该建筑物的高度.(取 =1.732,结果精确到1m)
=1.732,结果精确到1m)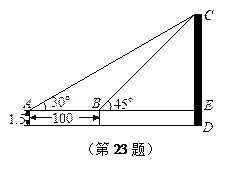
省射击队为从甲、乙两名运动员中选拔一人参加全国比赛,对
他们进行了六次测试,测试成绩如下表(单位:环):
| 第一次 |
第二次 |
第三次 |
第四次 |
第五次 |
第六次 |
|
| 甲 |
10 |
8 |
9 |
8 |
10 |
9 |
| 乙 |
10 |
7 |
10 |
10 |
9 |
8 |
(1)根据表格中的数据,计算出甲的平均成绩是环,乙的平均成绩是环;
(2)分别计算甲、乙六次测试成绩的方差;
(3)根据(1)、(2)计算的结果,你认为推荐谁参加全国比赛更合适,请说明理由.
(计算方差的公式:s2= [
[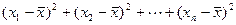 ])
])
试题篮
()