初中数学解答题

如图，在锐角△ABC中，AC是最短边；以AC中点O为圆心，AC长为半径作⊙O，交BC于E，过O作OD∥BC交⊙O于D，连结AE、AD、DC．
（1）求证：D是 弧AE 的中点；
（2）求证：∠DAO =∠B+∠BAD；
（3）若 ，且AC=4，求CF的长.

某校志愿者团队在重阳节购买了一批牛奶到“夕阳红”敬老院
慰问孤寡老人，如果给每个老人分5盒，则剩下38盒，如果给每个老人分6盒，则最后一
个老人不足5盒，但至少分得一盒．
（1）设敬老院有名老人，则这批牛奶共有多少盒？（用含的代数式表示）．
（2）该敬老院至少有多少名老人？最多有多少名老人？

某市为争创全国文明卫生城，2008年市政府对市区绿化工程投
入的资金是2000万元，2010年投入的资金是2420万元，且从2008年到2010年，两年间
每年投入资金的年平均增长率相同.
（1）求该市对市区绿化工程投入资金的年平均增长率；
（2）若投入资金的年平均增长率不变，那么该市在2012年需投入多少万元？

本题满分8分）“初中生骑电动车上学”的现象越来越受到社会的关注，某校利用“五一”假期，随机抽查了本校若干名学生和部分家长对“初中生骑电动车上学”现象的看法，统计整理制作了如下的统计图，请回答下列问题：
（1）这次抽查的家长总人数为；
（2）请补全条形统计图和扇形统计图；
（3）从这次接受调查的学生中，随机抽查一个学生恰好抽到持“无所谓”态度的概率
是．

本题满分8分）求证：角平分线上的点到这个角的两边距离相等.
已知：
求证：
证明：

解二元一次方程组：

如图所示，过点F（0，1）的直线y=kx＋b与抛物线交于M（x₁，y₁）
和N（x₂，y₂）两点（其中x₁＜0，x₂＜0）．
⑴求b的值．
⑵求x₁•x₂的值
⑶分别过M、N作直线l：y=－1的垂线，垂足分别是M₁、N₁，判断△M₁FN₁的形状，并证明你的结论．
⑷对于过点F的任意直线MN，是否存在一条定直线m，使m与以MN为直径的圆相切．如果有，请法度出这条直线m的解析式；如果没有，请说明理由．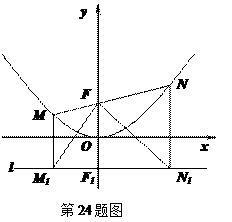

我市某镇的一种特产由于运输原因，长期只能在当地销售．当地政府对该特产的
销售投资收益为：每投入x万元，可获得利润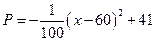（万元）．当地政府
拟在“十二•五”规划中加快开发该特产的销售，其规划方案为：在规划前后对该项目每年
最多可投入100万元的销售投资，在实施规划5年的前两年中，每年都从100万元中拨出
50万元用于修建一条公路，两年修成，通车前该特产只能在当地销售；公路通车后的3年
中，该特产既在本地销售，也在外地销售．在外地销售的投资收益为：每投入x万元，可获
利润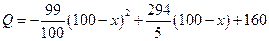（万元）
⑴若不进行开发，求5年所获利润的最大值是多少？
⑵若按规划实施，求5年所获利润（扣除修路后）的最大值是多少？
⑶根据⑴、⑵，该方案是否具有实施价值？

在圆内接四边形ABCD中，CD为∠BCA外角的平分线，F为弧AD上一点，
BC=AF，延长DF与BA的延长线交于E．
⑴求证△ABD为等腰三角形．
⑵求证AC•AF=DF•FE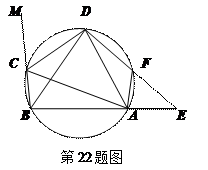

如图，防洪大堤的横断面是梯形，背水坡AB的坡比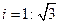（指坡面的铅直
高度与水平宽度的比）．且AB="20" m．身高为1.7 m的小明站在大堤A点，测得高压电
线杆端点D的仰角为30°．已知地面CB宽30 m，求高压电线杆CD的高度（结果保
留三个有效数字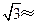，1.732）.

今年我省干旱灾情严重，甲地急需要抗旱用水15万吨，乙地13万吨．现有A、
B两水库各调出14万吨水支援甲、乙两地抗旱．从A地到甲地50千米，到乙地30千米；
从B地到甲地60千米，到乙地45千米．
⑴设从A水库调往甲地的水量为x万吨，完成下表

调出地 水量/万吨 调入地	甲	乙	总计
A	x		14
B			14
总计	15	13	28

⑵请设计一个调运方案，使水的调运量尽可能小．（调运量=调运水的重量×调运的距离，单位：万吨•千米）

有3张扑克牌，分别是红桃3、红桃4和黑桃5．把牌洗匀后甲先抽取一张，记
下花色和数字后将牌放回，洗匀后乙再抽取一张．
⑴先后两次抽得的数字分别记为s和t，则︱s－t︱≥1的概率．
⑵甲、乙两人做游戏，现有两种方案．A方案：若两次抽得相同花色则甲胜，否则乙胜．B方案：若两次抽得数字和为奇数则甲胜，否则乙胜．
请问甲选择哪种方案胜率更高？

如图，在等腰三角形ABC中，∠ABC=90°，D为AC边上中点，过D
点作DE⊥DF，交AB于E，交BC于F，若AE=4，FC=3，求EF长．

为了加强食品安全管理，有关部门对某大型超市的甲、乙两种品牌食用油共抽
18瓶进行检测，检测结果分成“优秀”、“合格”、“不合格”三个等级，数据处理后制成以
下折线统计图和扇形统计图．
⑴甲、乙两种品牌食用油各被抽取了多少瓶用于检测？
⑵在该超市购买一瓶乙品牌食用油，请估计能买到“优秀”等级的概率是多少？

如图，已知抛物线y=x²＋bx＋c与x轴交于A、B两点（A点在B点左侧），与y
轴交于点C（0，－3），对称轴是直线x=1，直线BC与抛物线的对称轴交于点D．
⑴求抛物线的函数表达式；
⑵求直线BC的函数表达式；
⑶点E为y轴上一动点，CE的垂直平分线交CE于点F，交抛物线于P、Q两点，且点P在第三象限．
①当线段PQ=AB时，求tan∠CED的值；
②当以点C、D、E为顶点的三角形是直角三角形时，请直接写出点P的坐标．
温馨提示：考生可以根据第⑶问的题意，在图中补出图形，以便作答．