某体育用品商店为了解8月份的销售情况,对本月各类商品的销售情况进行调查,并将调查的结果绘制成如下的两幅不完整的统计图.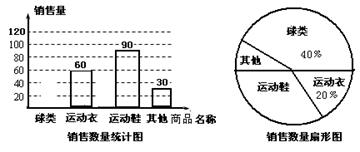
(1)请根据图中提供的信息,将条形图补充完整;
(2)该商店准备按8月份球类商品销量的数量购进球类商品,含篮球、足球、排球三种
球,预计恰好用完货款共3600元.设购进篮球x个,足球y个,三种球的进价和售
价如下表:
| 类别 |
篮球 |
足球 |
排球 |
| 进价(单位:元/个) |
50 |
30 |
20 |
| 预售价(单位:元/个) |
70 |
45 |
25 |
求出y与x之间的函数关系式;
(3)在(2)中的进价和售价的条件下,据实际情况,预计足球销售超过60个后,这种
球就会产生滞销,①假设所购进篮球、足球、排球能全部售出,求出预估利润P(元)与x(个)的函数关系式;②求出预估利润的最大值,并写出此时购进三种球各多少个?
(1)如图1,直线 //
// //
// //
// ,且
,且 与
与 ,
, 与
与 之间的距离均为1,
之间的距离均为1, 与
与 之间的距离为2,现将正方形ABCD如图放置,使其四个顶点分别在四条直线上,求正方形的边长;
之间的距离为2,现将正方形ABCD如图放置,使其四个顶点分别在四条直线上,求正方形的边长;
(2)在(1)的条件下,探究:将正方形ABCD改为菱形ABCD,如图2,当 时,求菱形的边长.
时,求菱形的边长.
如图,已知抛物线C1与坐标轴的交点依次是A(-4,0),B(-2,0),E(0,8).
(1)求抛物线C1关于原点对称的抛物线C2的解析式;
(2)设抛物线C1的顶点为M,抛物线C2与x轴分别交于C,D两点(点C在点D的左侧),顶点为N,四边形MDNA的面积为S.若点A,点D同时以每秒1个单位的速度沿水平方向分别向右、向左运动;与此同时,点M,点N同时以每秒2个单位的速度沿坚直方向分别向下、向上运动,直到点A与点D重合为止.求出四边形MDNA的面积S与运动时间t之间的关系式,并写出自变量t的取值范围;
(3)当t为何值时,四边形MDNA的面积S有最大值,并求出此最大值;
(4)在运动过程中,四边形MDNA能否形成矩形?若能,求出此时t的值;若不能,请说明理由.
如图,在平面直角坐标系中,抛物线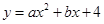 经过A(-3,0)、B(4,0)两点,且与y轴交于点C,D(
经过A(-3,0)、B(4,0)两点,且与y轴交于点C,D( ,0).动点P从点A出发,沿线段AB以每秒1个单位长度的速度向点B移动,同时动点Q从点C出发,沿线段CA以某一速度向点A移动.
,0).动点P从点A出发,沿线段AB以每秒1个单位长度的速度向点B移动,同时动点Q从点C出发,沿线段CA以某一速度向点A移动.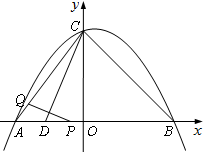
(1)求该抛物线的解析式;
(2)若经过t秒的移动,线段PQ被CD垂直平分,求此时t的值;
(3)在第一象限的抛物线上取一点G,使得S△GCB=S△GCA,再在抛物线上找点E(不与点A、B、C重合),使得∠GBE=45°,求E点的坐标.
已知:如图1,抛物线的顶点为M,平行于x轴的直线与该抛物线交于点A,B(点A在点B左侧),根据对称性△AMB恒为等腰三角形,我们规定:当△AMB为直角三角形时,就称△AMB为该抛物线的“完美三角形”.
(1)①如图2,求出抛物线 的“完美三角形”斜边AB的长;
的“完美三角形”斜边AB的长;
②抛物线 与
与 的“完美三角形”的斜边长的数量关系是 ;
的“完美三角形”的斜边长的数量关系是 ;
(2)若抛物线 的“完美三角形”的斜边长为4,求a的值;
的“完美三角形”的斜边长为4,求a的值;
(3)若抛物线 的“完美三角形”斜边长为n,且
的“完美三角形”斜边长为n,且 的最大值为-1,求m,n的值.
的最大值为-1,求m,n的值.
如图,矩形ABCD中,点O为AC的中点,过点O的直线分别与AB,CD交于点E,F,连接BF交AC于点M,连接DE,BO.若∠COB=60°,FO=FC.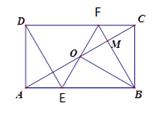
求证:(1)四边形EBFD是菱形; (2)MB : OE=3:2 .
(本题12分)某学校为了增强学生体质,决定开设以下体育课外活动项目:A 篮球,B 乒乓球,C 羽毛球,D 足球,为了解学生最喜欢哪一种活动项目,随机抽取了部分学生进行调查,并将调查结果绘制成了两幅不完整的统计图。请回答下列问题:
(1)这次被调查的学生共有 人;
(2)请你将条形统计图2补充完整;
(3)在平时的乒乓球项目训练中,甲、乙、丙、丁四人表现优秀,现决定从这四名同学中任选两名参加乒乓球比赛,求恰好选中甲、乙两位同学的概率。(用树状图或列表法解答)
(本小题满分11分)如图,E、F分别是正方形ABCD的边DC、CB上的点,且DE=CF,以AE为边作正方形AEHG,HE与BC交于点Q,连接DF.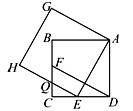
(1)求证:△ADE≌△DCF;
(2)若E是CD的中点,求证:Q为CF的中点;
(3)连接AQ,设S△CEQ=S1,S△AED=S2,S△EAQ=S3,在(2)的条件下,判断S1+S2=S3是否成立?并说明理由.
(本题12分)如图,ABCD是一张矩形纸片,AD=BC=1,AB=CD=5.在矩形ABCD的边AB上取一点M,在CD上取一点N,将纸片沿MN折叠,使MB与DN交于点K,得到△MNK.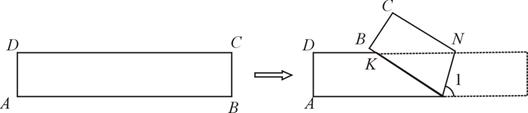
(1)若∠1=70°,求∠MKN的度数.
(2)△MNK的面积能否小于 ?若能,求出此时∠1的度数;若不能,试说明理由.
?若能,求出此时∠1的度数;若不能,试说明理由.
(3)如何折叠能够使△MNK的面积最大?请你利用备用图探究可能出现的情况,求出最大值.
如图,Rt△ 中,
中, ,
, ,
,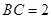 ,
,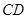 是斜边
是斜边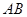 上的高,点
上的高,点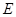 为边
为边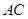 上一点(点
上一点(点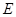 不与点
不与点 、
、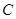 重合),连接
重合),连接 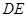 ,作
,作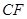 ⊥
⊥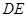 ,
,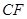 与边
与边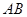 、线段
、线段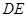 分别交于点
分别交于点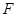 ,
, ;
;
(1)求线段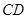 、
、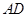 的长;
的长;
(2)设 ,
,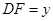 ,求
,求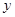 关于
关于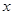 的函数解析式,并写出x的取值范围.
的函数解析式,并写出x的取值范围.
已知,如图,直线MN交⊙O于A,B两点,AC是直径,AD平分∠CAM交⊙O于D,过D作DE⊥MN于E.
(1)求证:DE是⊙O的切线;
(2)若DE=6cm,AE=3cm,求⊙O的半径.
选做题:从甲、乙两题中选做一题,如果两题都做,只以甲题计分。
题甲:如图,AB是⊙O的直径,经过圆上点D的直线CD恰使∠ADC=∠B.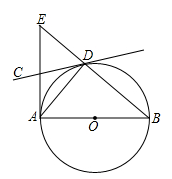
(1)求证:直线CD 是⊙O的切线;
(2)过点A作直线AB的垂线交BD的延长线于点E,且AB= ,BD=2,求S△ABE的面积
,BD=2,求S△ABE的面积
题乙:已知:一元二次方程x2﹣ax﹣3= 0
(1)求证:无论a取何值关于x的一元二次方程总有不等的实根。
(2)如果m,n是方程的两根且m2+n2=22试求a的值
如图,在平面直角坐标系中,已知点A的坐标是(4,0),并且OA=OC=4OB,动点P在过A,B,C三点的抛物线上.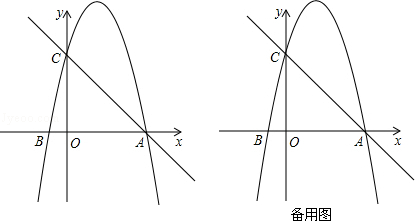
(1)求抛物线的解析式;
(2)是否存在点P,使得△ACP是以AC为直角边的直角三角形?若存在,求出所有符合条件的点P的坐标;若不存在,说明理由;
(3)过动点P作PE垂直于y轴于点E,交直线AC于点D,过点D作x轴的垂线.垂足为F,连接EF,当线段EF的长度最短时,求出点P的坐标.
随着生活质量的提高,人们健康意识逐渐增强,安装净水设备的百姓家庭越来越多.某厂家从去年开始投入生产净水器,生产净水器的总量y(台)与今年的生产天数x(天)的关系如图所示.今年生产90天后,厂家改进了技术,平均每天的生产数量达到30台.
(1)求y与x之间的函数表达式;
(2)已知该厂家去年平均每天的生产数量与今年前90天平均每天的生产数量相同,求厂家去年生产的天数;
(3)如果厂家制定总量不少于6000台的生产计划,那么在改进技术后,至少还要多少天完成生产计划?
(本小题满分10分)设抛物线 与x轴交于两个不同的点A(一1,0)B(4,0),与y轴交于点C.
与x轴交于两个不同的点A(一1,0)B(4,0),与y轴交于点C.
(1)求抛物线的解析式及∠ACB的度数;
(2)已知点D(1,n )在抛物线上,过点A的直线 交抛物线于另一点E.若点P在x轴上,以点P、B、D为顶点的三角形与△AEB相似,求点P的坐标.
交抛物线于另一点E.若点P在x轴上,以点P、B、D为顶点的三角形与△AEB相似,求点P的坐标.
试题篮
()