二次函数
的图象经过点（﹣1，4），且与直线
相交于A、B两点（如图），A点在y轴上，过点B作BC⊥x轴，垂足为点C（﹣3，0）．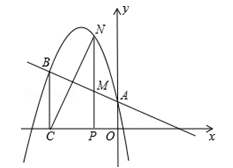
（1）求二次函数的表达式；
（2）点N是二次函数图象上一点（点N在AB上方），过N作NP⊥x轴，垂足为点P，交AB于点M，求MN的最大值；
如图，四边形ABCD内接于⊙O，BD是⊙O的直径，AE⊥CD，垂足为E，DA平分∠BDE．
（1）求证：AE是⊙O的切线；
（2）若∠DBC=30°，DE=1㎝，求BD的长．
某工厂生产的某种产品按质量分为10个档次，第1档次（最低档次）的产品一天能生产95件，每件利润6元．每提高一个档次，每件利润增加2元，但一天产量减少5件．
（1）若生产第x档次的产品一天的总利润为y元（其中x为正整数，且1≤x≤10），求出y关于x的函数关系式；
（2）若生产第x档次的产品一天的总利润为1120元，求该产品的质量档次．
如果二次函数的二次项系数为l，则此二次函数可表示为
，我们称[p，q]为此函数的特征数，如函数
的特征数是[2，3]．
（1）若一个函数的特征数为[﹣2，1]，求此函数图象的顶点坐标．
（2）若一个函数的特征数为[4，﹣1]，将此函数的图象先向右平移1个单位，再向上平移1个单位，求得到的图象对应的函数的特征数．
请同学们认真阅读下面的一段文字材料，然后解答题目中提出的有关问题．
为解方程
，我们可以将
视为一个整体，然后设
，则原方程可化为
①
解得
，
，当y=1时，
，∴
，
；
当y=4时，
，∴
，
，∴原方程的解为
=
，
=－，
=
，
=－．
解答问题：
（1）填空：在由原方程得到方程①的过程中，利用_________法达到了降次的目的，体现了_________的数学思想．
（2）解方程
．
如图，在平面直角坐标系中，三角形②、③是由三角形①依次旋转后所得的图形．
（1）在图中标出旋转中心P的位置，并写出它的坐标；
（2）在图上画出再次旋转后的三角形④．
如图，若将△ABC绕点O顺时针旋转180°后得到△A′B′C′，则A点的对应点A′点的坐标是____________．
如图，抛物线
经过点（1，﹣4）和（﹣2，5），请解答下列问题：
（1）求抛物线的解析式；
（2）若与x轴的两个交点为A，B，与y轴交于点C．在该抛物线上是否存在点D，使得△ABC与△ABD全等？若存在，求出D点的坐标；若不存在，请说明理由．
注：抛物线
的对称轴是
．
如图，AB是⊙O的直径，点F，C是⊙O上两点，且
，连接AC，AF，过点C作CD⊥AF交AF延长线于点D，垂足为D．
（1）求证：CD是⊙O的切线；
（2）若CD=
，求⊙O的半径．
如图，AD为△ABC外接圆的直径，AD⊥BC，垂足为点F，∠ABC的平分线交AD于点E，连接BD，CD．
（1）求证：BD=CD；
（2）请判断B，E，C三点是否在以D为圆心，以DB为半径的圆上？并说明理由．
四边形ABCD是正方形，E、F分别是DC和CB的延长线上的点，且DE=BF，连接AE、AF、EF．
（1）试判断△AEF的形状，并说明理由；
（2）填空：△ABF可以由△ADE绕旋转中心 点，按顺时针方向旋转 度得到；
（3）若BC=8，则四边形AECF的面积为 ．（直接写结果）
如图，抛物线
的图象与x轴交于A，B两点（点A在点B的左边），与y轴交于点C，点D为抛物线的顶点．
（1）求点A，B，C的坐标；
（2）点M为线段AB上一点（点M不与点A，B重合），过点M作x轴的垂线，与直线AC交于点E，与抛物线交于点P，过点P作PQ∥AB交抛物线于点Q，过点Q作QN⊥x轴于点N，若点P在点Q左边，当矩形PMNQ的周长最大时，求△AEM的面积；
（3）在（2）的条件下，当矩形PMNQ的周长最大时，连接DQ，过抛物线上一点F作y轴的平行线，与直线AC交于点G（点G在点F的上方）．若FG＝
DQ，求点F的坐标．
已知直线l与⊙O，AB是⊙O的直径，AD⊥l于点D．
（1）如图①，当直线l与⊙O 相切于点C时，若∠DAC＝30°，求∠BAC的大小；
（2）如图②，当直线l与⊙O 相交于点E、F时，若∠DAE＝18°，求∠BAF的大小．
某文具店销售一种进价为每本10元的笔记本，为获得高利润，以不低于进价进行销售，结果发现，每月销售量y与销售单价x之间的关系可以近似地看作一次函数：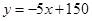
，物价部门规定这种笔记本每本的销售单价不得高于18元．
（1）当每月销售量为70本时，获得的利润为多少元；
（2）该文具店这种笔记本每月获得利润为w元，求每月获得的利润w元与销售单价x之间的函数关系式，并写出自变量的取值范围；
（3）当销售单价定为多少元时，每月可获得最大利润，最大利润为多少元？
试题篮
()
粤公网安备 44130202000953号
，连接AC，AF，过点C作CD⊥AF交AF延长线于点D，垂足为D．
，求⊙O的半径．