如图,“和谐号”高铁列车的小桌板收起时近似看作与地面垂直,小桌板的支
架底端与桌面顶端的距离OA = 75厘米.展开小桌板使桌面保持水平,此时CB⊥AO,∠AOB =∠ACB = 37°,
且支架长OB与桌面宽BC的长度之和等于OA的长度.求小桌板桌面的宽度BC.
(参考数据sin37° ≈ 0.6,cos37° ≈ 0.8,tan37° ≈ 0.75)


如图,菱形ABCD的对角线AC、BD相交于点E,F是BA延长线上一点,连接EF,以EF为直径作⊙O,交DC于D、G两点,AD分别与EF,GF交于I、H两点.
(1)求证:AE∥FD;
(2)试判断AF和AB的数量关系,并证明你的结论;
(3)当G为线段DC的中点时,
①求证:AE=IE;
②设AC=12,BC=10,求GF的长.
如图,正方形ABCD的边长为4cm,点E、F在边AD上运动,且AE=DF.CF交BD于G,BE交AG于H.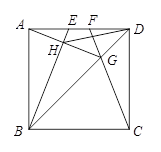
(1)求证:∠DAG=∠ABE;
(2)①求证:点H总在以AB为直径的圆弧上;
②画出点H所在的圆弧,并说明这个圆弧
的两个端点字母;
(3)直接写出线段DH长度的最小值.
如图,AB是⊙O的切线,切点为B,AO交⊙O于点C,点D在AB上,且DB=DC.
(1)求证:DC为⊙O的切线.
(2)若AD=2BD,CD=2,求⊙O的半径.
已知关于x的一元二次方程x2-(k+2)x+2k=0.
(1)试说明:无论k取何值时,这个方程一定有实数根;
(2)若等腰△ABC的一边长a=1,另两边长b、c恰好是这个方程的两个根,求△ABC的周长.
如图,⊙O的直径AB⊥弦CD,垂足为E,连接AD、OC、OD,且OD=5.
(1)若CD=8,求AD长;
(2)若∠ADO:∠EDO=4:1,求扇形OAC(阴影部分)的面积(结果保留π).
某中学开展歌咏比赛,九年级(1)、(2)班根据初赛成绩,各选出5名选手参加复赛的成绩(满分为100分)如图所示.

(1)根据图示填写下表;
| 班级 |
平均数 |
中位数 |
众数 |
| 九(1) |
|
85 |
|
| 九(2) |
85 |
|
100 |
(2)计算两班复赛成绩的方差,并分析哪个班级的复赛成绩稳定.
某商场销售一批衬衫,平均每天可售出20件,每件盈利44元.为了扩大销售,增加盈利,商场采取降价措施.假设在一定范围内,衬衫单价降1元,商场平均每天可多售出5件.如果商场通过销售这批衬衫每天盈利1600元,那么衬衫的单价应降多少元?
一只不透明的袋子中装有2个白球和1个红球,这些球除颜色外都相同,搅匀后从中任意摸出1个球,记录颜色后放回、搅匀,再从中任意摸出1个球.
(1)请用画树状图或列表的方法列出所有可能出现的结果;
(2)求两次都摸到白球的概率.
操作题:如图,△ABC内接于⊙O,AB=AC,P是⊙O上一点.
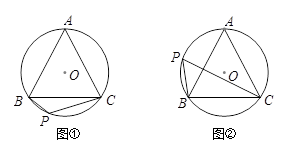
(1)请你只用无刻度的直尺,分别画出图①和图②中∠P的平分线;
(2)结合图②,说明你这样画的理由.
试题篮
()