如图,将正方形纸片 沿 折叠,使点 的对称点 落在边 上,点 的对称点为点 , 交 于点 ,连接 交 于点 ,连接 .下列四个结论中:① ;② ;③ 平分 ;④ ,正确的是 (填序号即可).

如图,在边长为 的正六边形 中,连接 , ,其中点 , 分别为 和 上的动点.若以 , , 为顶点的三角形是等边三角形,且边长为整数,则该等边三角形的边长为 .

将黑色圆点按如图所示的规律进行排列:

图中黑色圆点的个数依次为:1,3,6,10, ,将其中所有能被3整除的数按从小到大的顺序重新排列成一组新数据,则新数据中的第33个数为 .
如图,在矩形 中, , , 、 分别是边 、 上一点, ,将 沿 翻折得△ ,连接 ,当 时, 是以 为腰的等腰三角形.

如图,在平面直角坐标系中, 为坐标原点,点 为 轴正半轴上的一个动点,过点 的直线与二次函数 的图象交于 、 两点,且 , 为 的中点,设点 的坐标为 , ,写出 关于 的函数表达式为: .

如图,射线 , 互相垂直, ,点 位于射线 的上方,且在线段 的垂直平分线 上,连接 , .把线段 绕点 按逆时针方向旋转得到对应线段 ,若点 恰好落在射线 上,则点 到射线 的距离 .
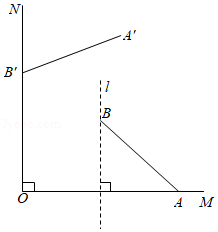
如图,在 中, , , , 是 上一点(点 与点 不重合).若在 的直角边上存在4个不同的点分别和点 、 成为直角三角形的三个顶点,则 长的取值范围是 .

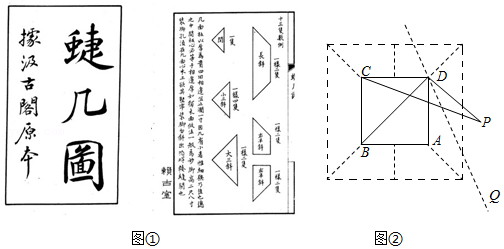
《蝶几图》是明朝人戈汕所作的一部组合家具的设计图
"  "为"蜨",同"蝶"
,它的基本组件为斜角形,包括长斜两只、右半斜两只、左半斜两只、闺一只、小三斜四只、大三斜两只,共十三只(图①中的"樣"和"隻"为"样"和"只"
.图②为某蝶几设计图,其中
和
为"大三斜"组件
"一樣二隻"的大三斜组件为两个全等的等腰直角三角形),已知某人位于点
处,点
与点
关于直线
对称,连接
、
.若
,则
度.
"为"蜨",同"蝶"
,它的基本组件为斜角形,包括长斜两只、右半斜两只、左半斜两只、闺一只、小三斜四只、大三斜两只,共十三只(图①中的"樣"和"隻"为"样"和"只"
.图②为某蝶几设计图,其中
和
为"大三斜"组件
"一樣二隻"的大三斜组件为两个全等的等腰直角三角形),已知某人位于点
处,点
与点
关于直线
对称,连接
、
.若
,则
度.
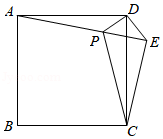
如图,在正方形 外取一点 ,连接 , , ,过点 作 的垂线交 于点 ,若 , .下列结论:① ;② ;③点 到直线 的距离为 ;④ ,其中正确结论的序号为 .
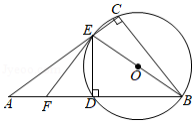
如图,在 中, , 的垂直平分线分别交 、 于点 、 , , 为 的外接圆,过点 作 的切线 交 于点 ,则下列结论正确的是 (写出所有正确结论的序号)
① ;
② ;
③若 ,则 的长为 ;
④ ;
⑤若 ,则 .
试题篮
()