如图所示,有两只完全相同的溢水杯分别盛有密度不同的A、B两种液体,将两个体积均为V,所受重力分别为GC 、GD的小球C、D分别放入两容器中,当两球静止时,两杯中液面相平,且C球有一半体积浸入液体中,D球全部浸入液体中。此时两种液体对甲、乙两容器底部的压强分别为pA、pB ;甲、乙两容器对桌面的压强分别为p1、p2。要使C球刚好完全没入液体中,须对C球施加竖直向下的压力F,若用与F同样大小的力竖直向上提D球,可使它有V1的体积露出液面。已知C、D两球的密度比为2:3。则下述判断正确的是
A.p1>p2 ;2GC =3GD
B.3p1=4p2 ;pA>pB
C.3GC =2GD;3V1 ="2" V
D.3pA=4pB ;3V1 = V
三个完全相同的杯子里装有同样多的水,把质量都为300g的铝块、铁块、铜块分别浸没在这三杯水中(水均未溢出),则水面最高的是(ρ铝<ρ铁<ρ铜)( )
| A.放入铝块的杯子 | B.放入铁块的杯子 | C.放入铜块的杯子 | D.无法确定 |
世界上密度最小的固体“气凝胶”是人类探索新材料取得的重要成果.该物质的坚固耐用程度不亚于钢材,且能承受1400℃的高温,而密度只有3kg/m3。一架用钢材(ρ钢=7.9×103kg/m3)制成的质量约160t的大型飞机,如果用“气凝胶”做成,其质量大约是
| A.几千克 | B.几十千克 |
| C.几百千克 | D.几千千克 |
如图所示,有两圆柱形容器底面积之比2:3,装有质量不等的水。将密度为0.6×103千克/米3的木块甲放入A容器中,将物块乙浸没在乙容器的水中,且均不溢出,要求:水对容器底部压强变化量相等,则判断甲、乙的体积关系: 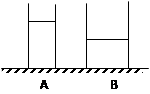
A、V甲>V乙 B、V甲 < V乙
C、V甲=V乙 D、无法判断
甲、乙、丙三个相同柱状容器内分别盛有质量相等的不同液体,将质量相等的实心铜、铁、铝球(已知ρ铜>ρ铁>ρ铝)分别浸没在液体中,此时液面等高,则液体对容器底的压强( )
| A.p甲<p乙<p丙 | B.p甲=p乙=p丙 | C.p甲>p乙>p丙 | D.p甲=p乙>p丙 |
一个质量为0.25千克的玻璃瓶,盛满水时称得质量是1.5千克,若盛满某液体时称得质量是1.75千克,那么某液体的密度是 ( )
| A.1.75×103千克/米3 | B.1.2×103千克/米3 |
| C.1.16×103千克/米3 | D.1.0×103千克/米3 |
用量杯盛某种液体,测得液体体积V和液体与量杯共同质量m的关系如图所示,从图中可知( )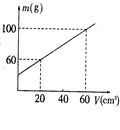
A.该液体的密度是3g /cm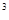 |
B.量杯的质量40g |
| C.体积为60ml时液体质量为100g | D.该液体可能是酒精 |
三个完全相同的杯子都装满了水,将质量相同的实心铜球、铁球和铝球分别放入三个杯中,都浸没时溢出水最多的是放入了(已知ρ铜>ρ铁>ρ铝)( )
| A.铜球 | B.铁球 | C.铝球 | D.不能确定 |
王兵在“测量石块的密度”时,测出几组数据,根据这些数据绘出图象,如图6四幅图象中,能正确表示石块“质量与体积的关系”的图象是 ,能正确表示“密度与质量的关系”的图象是 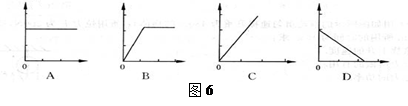
几种燃料的密度见下表.三辆完全相同的油罐车,分别盛满这三种燃料,下列说法正确的是( )
 |
柴油 |
煤油 |
汽油 |
| 密度ρ/kg·m-3 |
0.85×103 |
0.80×103 |
0.71×103 |
| 油罐车编号 |
甲 |
乙 |
丙 |
A.三车质量相同 B.甲车质量最大
C.乙车质量最大 D.丙车质量最大
三个完全相同的杯子里面装有水,把质量相同的实心铜块、铁块、铝块(密度大小关系见密度表)依次放在甲、乙、丙三个杯子中,水面恰好相平,原来装水最多的杯子是 ( )
| A.甲杯 | B.乙杯 | C.丙杯 | D.原来装水一样 |
有空心的铜球、铁球和铝球各一个,外观体积和质量都相等,这三个球空心部分最小的是:( )(已知ρ铜>ρ铁>ρ铝 )
| A.铜球 | B.铁球 | C.铝球 | D.一样大 |
甲物质的密度为5g/cm3,乙物质密度为2g/cm3,各取一定质量混合后密度为3g/cm3.假设混合前后总体积保持不变,则所取甲、乙两种物质的质量之比是( )
| A.5:2 | B.2:5 | C.5:4 | D.4:5 |
试题篮
()