初中物理探究杠杆的平衡条件实验试题

60kg的人站在跷跷板某一位置时，跷跷板处于如图所示的平衡状态。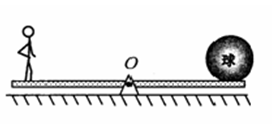

（1）由此可估测球的质量约为

A．20kg

B．30kg

C．60kg

D．120kg

（2）当人走向杠杆中点时，杠杆将向       倾斜（选题“左”或“右”）。

如图所示，将体积相同的物体G₁、G₂分别挂在杠杆的两端，杠杆处于平衡状态．若将两个物体G₁、G₂同时浸没在水中，则(　　)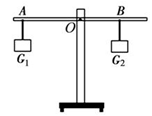

A．杠杆仍能保持平衡	B．杠杆不能平衡，A端下沉
C．杠杆不能平衡，B端下沉	D．无法确定杠杆的状态

如图所示，有一轻质木板（质量忽略不计），左端可绕O点转动，长为L，右端放一重为G的物块，并用一竖直向上的力F拉着.当物块向左匀速滑动时，木板始终在水平位置保持静止，则下列表示拉力F与物块运动时间t的关系图中，正确的是

如图所示，有一固定在墙壁上的可绕支点O转动杠杆，在杠杆上C点悬挂一装有水的敞口水杯，在A点施加竖直向上的拉力F使杠杆在水平位置保持平衡．则拔下水杯底部的塞子后，拉力F随时间t变化的图像是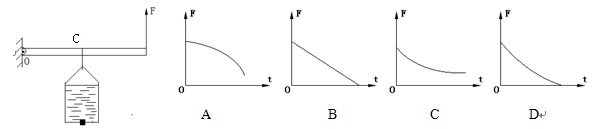

如图所示，用固定在墙上的三角支架ABC放置空调室外机.如果A处螺钉松脱，则支架会绕      (选填“A”、“ B”或“C”)点倾翻.已知AB长40cm，AC长30cm，室外机的重力为300N，正好处在AB中点处，则A处螺钉的水平拉力为     N（支架重力不计）.为了安全，室外机应尽量    （选填“靠近”或“远离”）墙壁.

质量相同的铁块和铝块，挂在杠杆AB两端，杠杆在水平位置平衡，如图所示，现把铁块和铝块同时浸没于水中，已知ρ_铁 >ρ_铝，则有

A．杠杆AB仍保持平衡	B．杠杆A端会上升以
C．杠杆Ａ端会下降	D．杠杆是否平衡，无法判断

如图所示，是“探究杠杆平衡条件”的装置图．
（1）实验前为方便测量力臂长度，应将杠杆调节到  平衡，如果杠杆的左端向下倾斜，平衡螺母应
向  端调节．
（2）实验记录的数据如表所示，收集多组数据的目的是       ；实验得到的结论是    （用字母符号表示）．

实验次数	动力F1/N	动力臂L1/cm	阻力F2/N	阻力臂L2/cm
1	0.5	10	1	5
2	0.5	15	1.5	5
3	1.5	20	3	10
4	2	20	4	10

（3）图中杠杆处于平衡状态，每个钩码受到的重力是0.5N，则弹簧测力计竖直向下的拉力是  N；拉着弹簧测力计，逐渐向右倾斜，并保持杠杆平衡，弹簧测力计的示数将    ．

如图是某型号起重机从水中调起一重7.9t的钢锭，L₁、L₂分别为2m、6m。(g取10N／kg，ρ_钢＝7.9×10³kg／m³) 求：

（1）钢锭全部浸在水中时受到的浮力是多大?
（2）起重机将钢锭调离水面后，起重机的作用力F₁是多大？
（3）调离水面后钢锭又匀速上升了3m，这个过程中起重机做的功为3.95×10⁵J，这时，起重机的机械效率是多少？

小梅在物理老师的指导下，利用一个重物、细线、若干钩码及杠杆来探究“杠杆平衡的条件”。

（1）实验前，为便于力臂的测量，她应通过调节杠杆两端的　　使杠杆在　　位置平衡。

（2）实验时，小梅决定先保持阻力 $F_2$和阻力臂 $l_2$不变，探究“杠杆平衡时，动力臂和动力之间的关系”。

于是，她用细线将重物固定到杠杆左侧某一位置处；然后在杠杆右侧用细线悬挂一个钩码，移动其悬挂的位置，使杠杆重新在水平位置平衡，如图所示，将动力 $F_1$和动力臂 $l_1$记录下来。

接下来，她要改变　　并移动其悬挂的位置，多次重复前面的实验，并把相应的数据记录下来。

（3）小梅通过实验得到的实验数据如表1所示。

表一 保持阻力 $F_2$和阻力臂 $l_2$不变，探究杠杆平衡时动力臂和动力之间的关系

实验序号	动力 $F_1/N$	动力臂 $l_1/m$
1	0.5	0.20
2	1.0	0.10
3	1.5	0.07
4	2.0	0.05
5	2.5	0.04

分析表1中的数据，小梅得出的结论是：保持阻力和阻力臂不变，杠杆平衡时，动力臂 $l_1$跟动力 $F_1$成　　关系。

（4）在前面实验的基础上，小梅进一步猜想：在更普遍的情况下，杠杆平衡时可能满足“动力 $F_1\times$动力臂 $l_1=$阻力臂 $F_2\times$阻力臂 $l_2$”

为了验证小梅的这个猜想，小丽通过实验得到的实验数据如表2所示

表2 探究杠杆平衡时，动力 $F_1$、动力臂 $l_1$和阻力 $F_2$、阻力臂 $l_2$之间的关系

实验次数	动力 $F_1/N$	动力臂 $l_1/m$	阻力 $F_2/N$	阻力臂 $l_2/m$
1	1.0	0.10	1.0	0.10
2	1.5	0.08	1.5	0.08
3	2.0	0.07	2.0	0.07

小梅认为，表2中小丽的实验数据缺乏普遍性，用来验证她的猜想不够充分，于是对小丽的实验和收集数据提出了具体的建议。

小梅的建议是：小丽还要在　　的情况下进行实验和收集数据。

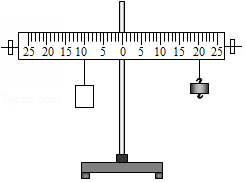
如图是一种自动测定油箱内油面高度的装置，R是滑动变阻器，它的金属滑片是杠杆的一端，且受定位挡板限制只能在电阻上滑动．当油面在A处时，滑动变阻器的滑片恰好在最下端；当油面在B处时，滑动变阻器的滑片在最上端．从油量表（由电流表改装而成）指针所指的刻度，可以知道油箱内油面的高度．现已知油的密度ρ=0.8×10³kg/m³，电源电压是6V，定值电阻R′的阻值是12Ω．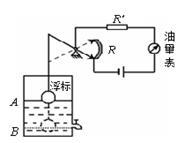

（1）若浮标有2×10^-4m³的体积浸入油中，则油对它的浮力是多大？（g取10N/kg）提示：F_浮=ρ_油gV_排
（2）当油面处在A处时，电流表示数为多少？
（3）已知电流增大时，电流表指针向右偏转，则＿＿＿＿＿．

A．油面下降时，电流表指针向右偏转

B．油量表零刻度线一定与电流表原零刻度线相重合

C．油量表的刻度值从左往右是逐渐增大的

D．油箱内的油越少，流过电流表的电流越大

如图所示，平直的薄板AB长1m，重力忽略不计，B端用细绳悬于天花板上，绳与水平方向夹角为30°，薄板始终保持水平.一辆重20N、功率为1W的电动小车，从A端以0.2m/s的速度向右匀速行驶4s，细绳恰好被拉断，求：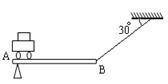

（1）小车行驶过程中牵引力做的功；
（2）小车运动时受到的阻力；
（3）细绳恰好被拉断时能承受的最大拉力.

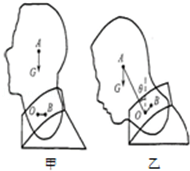
“低头族”长时间低头看手机，会引起颈部肌肉损伤．当头颅为竖直状态时，颈部肌肉的拉力为零，当头颅低下时，颈部肌肉会产生一定的拉力．为了研究颈部肌肉的拉力与低头角度大小的关系，我们可以建立一个头颅模型来模拟实验，如图甲所示．把人的颈椎简化成一个支点O，用1kg的头颅模型在重力作用下绕着这个支点O转动，A点为头颅模型的重心，B点为肌肉拉力作用点．将细线的一端固定在B点，用弹簧测力计拉着细线模拟测量肌肉的拉力，头颅模型在转动过程中，细线拉力的方向始终垂直于OB，如图乙所示．让头颅模型从竖直状态开始转动，通过实验记录出低头角度θ及细线拉力F的数据．如表：

低头角度θ/°	0	15	30	45	60
细线拉力F/N	0	7.3	14.0	20.2	25.0

（1）头颅模型质量为1kg，当低头角度为60°时，颈部肌肉实际承受的拉力是      N；如果真实头颅质量为8kg，当低头角度为60°时，颈部肌肉实际承受的拉力是      N．
（2）请解释：为什么低头角度越大，颈部肌肉的拉力会越大？答      ．
（3）请你就预防和延缓颈椎损伤提出一个合理化的建议：      ．

探究杠杆的平衡条件
【提出问题】如图所示，是一种常见的杆秤．此时处于水平位置平衡．

发现一：小明在左侧挂钩上增加物体，可观察到提纽左侧下沉．他认为改变杠杆的水平平衡可以通过改变作用在杠杆上的     来实现；
发现二；接着小新移动秤砣使其恢复水平位置平衡。说明通过改变        的长短也可以改变杠杆的平衡．
那么，杠杆在满足什么条件时才平衡呢?
【制定计划与设计实验】
实验前，轻质杠杆处于如图所示的状态，使用时，首先应将杠杆的平衡螺母向     （选填“左”或“右”）调节，使杠杆处于水平位置平衡，这样做的好处是          

【实验结论】
如图所示，他们进行了三次实验，对实验数据进行分析，得出杠杆的平衡条件是              ，

【拓展应用】如图所示，是用手托起重物的示意图，图中前臂可以看作是一个        杠杆（选填“省力”、“费力”或“等臂”），此杠杆的支点是图中的      点，假如托起6N的重物，请你根据图21所示，估算出手臂要用的动力大约是      N

在探究“杠杆平衡条件”的实验中：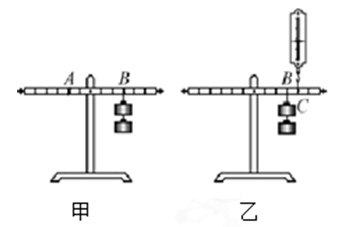

（1）某同学将杠杆悬挂起来，发现杠杆的右端低，左端高，他应该将杠杆两端的平衡螺母向________调节，使杠杆在________位置平衡。
（2）如图甲所示，在杠杆右边B处挂两个相同的钩码，要使杠杆仍在水平位置平衡，应在杠杆左边A处挂____个相同的钩码。
（3）如图乙所示，用弹簧测力计在C处竖直向上拉，当弹簧测力计逐渐向右倾斜时，杠杆仍然在水平位置平衡，弹簧测力计的拉力F_____（选填“变大”、“不变”或“变小”），原因是______。

某电开水器的结构如图甲所示（剖面图），简化的内部电路如图乙所示，进水管管口的阀门由轻质浮子1和与它们相连的两根轻质硬杆控制，只有进水管中的水压在正常范围内，冷水箱和煮水箱中的水位就比出水管管口低，冷水不会从出水管流出。当冷水箱中的水位达到一定高的时，浮子2浮起，会触动单刀三掷开关S₁，煮水电热管R₁通电发热，冷水被煮沸，水面升高，开水就从出水管进入贮水箱，当贮水箱中水位达到一定高度时，浮子3浮起，又会触动单刀三掷开关S₁，煮水暂停，一旦贮水箱中水温下降使温控开关S₂闭合，保温电热管R₂就会通电发热，开水处于保温状态。

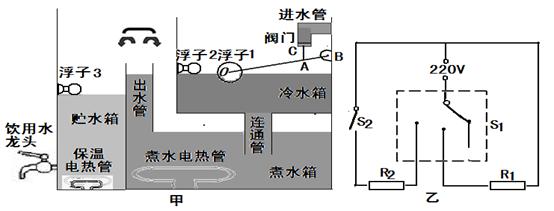
（1）已知煮水电热管R₁的阻值为12.1Ω，保温电热管R₂的阻值为48.4Ω，求电开水器的最大发热功率。
（2）图甲中，当浮子1上升到最高处后，它的最上端恰好和出水管管口相平，阀门就会将进水管管口关闭，此时AC杆沿竖直方向。已知浮子1的体积V=2.5×10^-4m³，进水管管口和阀门的横截面积S均为1×10^-4m²（不计阀门的质量、管壁的厚度及两者之间的摩擦）；BO∶BA=20∶1（O为轻质浮子1的球心、A为两轻质硬杆的相交处，B为轻质硬杆BO的转轴），水箱内水面上方的气压P₀=1×10⁵Pa。为了不让冷水直接进入贮水箱，进水管管口阀门的上表面受到的压强不能超过多少Pa?